Understanding the Z-Table: A Comprehensive Guide
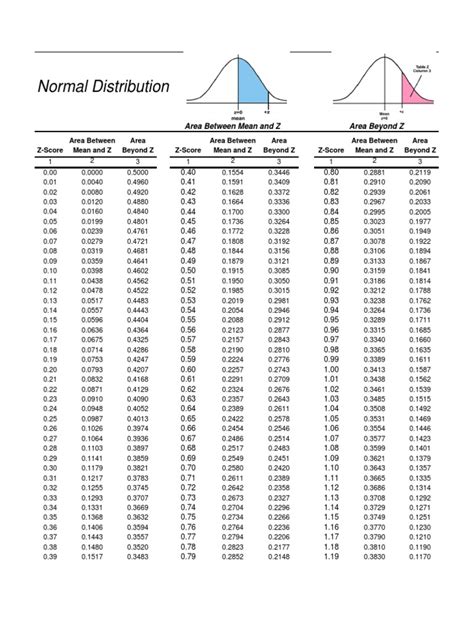
The Z-table, also known as the standard normal distribution table or Z-score table, is a statistical tool used to determine the probability of a value falling within a certain range in a standard normal distribution. The Z-table is essential in hypothesis testing, confidence intervals, and statistical analysis. In this article, we will delve into the world of Z-tables, exploring their significance, structure, and applications.
What is a Z-Table?
A Z-table is a table that lists the probabilities of a standard normal variable (Z) falling within a certain range. The Z-table is used to find the probability of a value being less than or equal to a given Z-score. The Z-score is a measure of how many standard deviations an observation is away from the mean. The Z-table is typically organized with Z-scores on the left-hand side and probabilities on the right-hand side.
How to Read a Z-Table
Reading a Z-table requires understanding the structure and layout of the table. The Z-table typically consists of rows and columns, where each row represents a Z-score and each column represents a probability. To read a Z-table, follow these steps:
- Identify the Z-score of interest and locate it in the left-hand column of the table.
- Move horizontally to the right to find the corresponding probability.
- The probability value represents the area under the standard normal curve to the left of the Z-score.
| Z-Score | Probability |
|---|---|
| -3.00 | 0.0013 |
| -2.00 | 0.0228 |
| -1.00 | 0.1587 |
| 0.00 | 0.5000 |
| 1.00 | 0.8413 |
| 2.00 | 0.9772 |
| 3.00 | 0.9987 |

Applications of Z-Tables
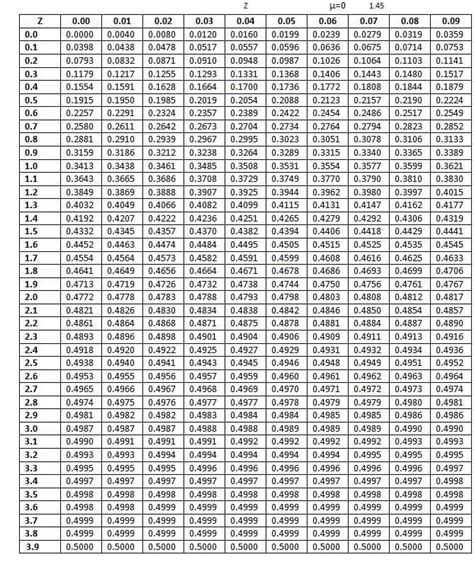
Z-tables have numerous applications in statistics, including:
Hypothesis Testing
Z-tables are used to determine the probability of a test statistic falling within a certain range, which is essential in hypothesis testing. By using a Z-table, researchers can calculate the probability of obtaining a test statistic at least as extreme as the one observed, assuming the null hypothesis is true.
Confidence Intervals
Z-tables are used to construct confidence intervals, which provide a range of values within which a population parameter is likely to lie. By using a Z-table, researchers can determine the probability of a confidence interval containing the true population parameter.
Statistical Analysis
Z-tables are used in various statistical analyses, including regression analysis, time series analysis, and survey research. By using a Z-table, researchers can calculate probabilities, construct confidence intervals, and test hypotheses.
Key Points
- The Z-table is a statistical tool used to determine the probability of a value falling within a certain range in a standard normal distribution.
- The Z-table is essential in hypothesis testing, confidence intervals, and statistical analysis.
- Reading a Z-table requires understanding the structure and layout of the table.
- Z-tables have numerous applications in statistics, including hypothesis testing, confidence intervals, and statistical analysis.
- Understanding Z-tables is crucial in making informed decisions in statistics and research.
Conclusion
In conclusion, the Z-table is a powerful tool in statistics, providing a way to determine the probability of a value falling within a certain range in a standard normal distribution. By understanding how to read and use a Z-table, researchers can make informed decisions in hypothesis testing, confidence intervals, and statistical analysis. Whether you’re a student or a professional, mastering the Z-table is essential in unlocking the secrets of statistical analysis.
What is the purpose of a Z-table?
+The purpose of a Z-table is to determine the probability of a value falling within a certain range in a standard normal distribution.
How do I read a Z-table?
+To read a Z-table, identify the Z-score of interest and locate it in the left-hand column of the table. Then, move horizontally to the right to find the corresponding probability.
What are the applications of Z-tables?
+Z-tables have numerous applications in statistics, including hypothesis testing, confidence intervals, and statistical analysis.
Meta description: Learn how to use a Z-table to determine the probability of a value falling within a certain range in a standard normal distribution. Understand the structure and layout of a Z-table and its applications in hypothesis testing, confidence intervals, and statistical analysis.


