Rational equations are a fundamental concept in algebra, and solving them is a crucial skill for any student or professional in mathematics and related fields. A rational equation is an equation that contains one or more rational expressions, which are fractions of polynomials. In this article, we will delve into the world of rational equations, exploring the different types, methods of solution, and practical applications.
Key Points
- Rational equations can be solved using various methods, including factoring, the rational root theorem, and cross-multiplication.
- The type of rational equation determines the most effective method of solution.
- Rational equations have numerous practical applications in fields such as physics, engineering, and economics.
- Graphing calculators and computer algebra systems can be used to visualize and solve rational equations.
- Understanding the concept of rational equations is essential for advanced mathematical topics, such as calculus and differential equations.
Types of Rational Equations
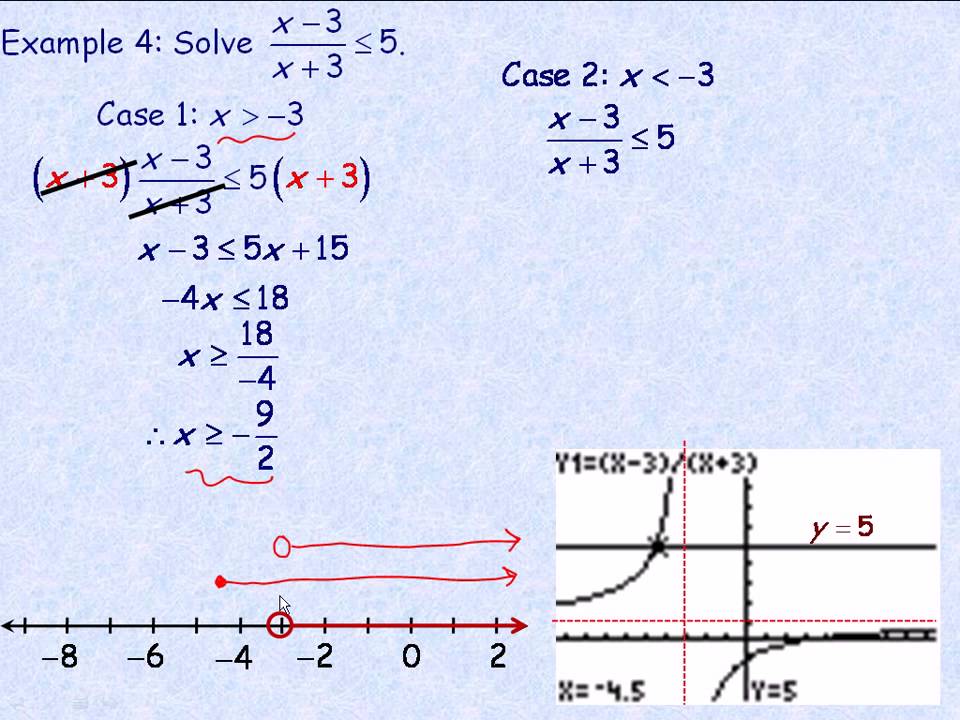
Rational equations can be categorized into several types, each with its unique characteristics and solution methods. The most common types of rational equations are:
- Proportional rational equations: These equations involve a single rational expression and can be solved by cross-multiplication.
- Non-proportional rational equations: These equations involve multiple rational expressions and require more advanced solution methods, such as factoring or the rational root theorem.
- Rational equations with quadratic expressions: These equations involve quadratic expressions in the numerator or denominator and require specialized solution methods, such as the quadratic formula.
Solution Methods
The method of solution for a rational equation depends on the type of equation and the level of complexity. Some common solution methods include:
Factoring: This method involves factoring the numerator and denominator of the rational expression to simplify the equation and solve for the unknown variable.
Rational root theorem: This method involves using the rational root theorem to identify potential rational roots of the equation and then testing these roots to find the solution.
Cross-multiplication: This method involves cross-multiplying the rational expressions to eliminate the fractions and solve for the unknown variable.
| Method | Description |
|---|---|
| Factoring | Factoring the numerator and denominator to simplify the equation |
| Rational root theorem | Using the rational root theorem to identify potential rational roots |
| Cross-multiplication | Cross-multiplying the rational expressions to eliminate fractions |

Practical Applications
Rational equations have numerous practical applications in fields such as physics, engineering, and economics. Some examples include:
- Optimization problems: Rational equations can be used to model optimization problems, such as maximizing profit or minimizing cost.
- Physics and engineering: Rational equations can be used to model real-world phenomena, such as the motion of objects or the behavior of electrical circuits.
- Economics: Rational equations can be used to model economic systems, such as the behavior of supply and demand curves.
Graphing Calculators and Computer Algebra Systems
Graphing calculators and computer algebra systems can be used to visualize and solve rational equations. These tools can help students and professionals to:
Graph rational equations: Graphing calculators and computer algebra systems can be used to graph rational equations, which can help to visualize the solution and identify any restrictions on the domain.
Solve rational equations: Graphing calculators and computer algebra systems can be used to solve rational equations, which can help to find the solution quickly and accurately.
What is the difference between a rational equation and a rational expression?
+A rational equation is an equation that contains one or more rational expressions, while a rational expression is a fraction of polynomials.
How do I solve a rational equation with a quadratic expression in the numerator or denominator?
+To solve a rational equation with a quadratic expression in the numerator or denominator, you can use specialized solution methods, such as the quadratic formula or factoring.
What are some common applications of rational equations in real-world problems?
+Rational equations have numerous practical applications in fields such as physics, engineering, and economics, including optimization problems, physics and engineering, and economics.
In conclusion, solving rational equations is a crucial skill for any student or professional in mathematics and related fields. By understanding the different types of rational equations, solution methods, and practical applications, individuals can develop a deeper appreciation for the importance of rational equations in real-world problems. Whether using graphing calculators and computer algebra systems or relying on traditional solution methods, solving rational equations requires a combination of mathematical knowledge, critical thinking, and problem-solving skills.



