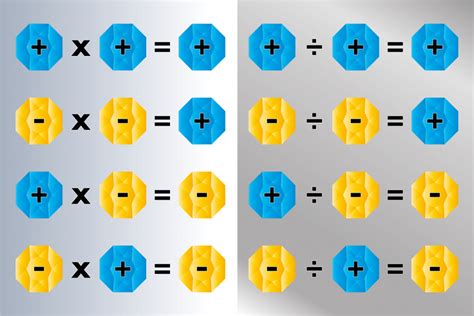
The concept of negative times positive is a fundamental aspect of mathematics, particularly in the realm of multiplication. When we multiply a negative number by a positive number, the result is always negative. This might seem counterintuitive at first, but it's essential to understand the underlying principles to grasp why this is the case. To delve into this concept, let's start with the basics of multiplication and how it applies to negative and positive numbers.
Understanding Multiplication with Negative and Positive Numbers

Multiplication is a mathematical operation that represents the repeated addition of a number. For instance, 3 multiplied by 4 (3 * 4) means adding 3 together 4 times, which equals 12. However, when we introduce negative numbers into this operation, things become a bit more complex. A negative number is essentially the opposite of a positive number. For example, -3 is the opposite of 3, and when you add -3 and 3 together, you get 0.
The Rule for Negative Times Positive
The rule for multiplying a negative number by a positive number is straightforward: the result is always negative. This can be represented as (-a) * b = -ab, where “a” and “b” are positive numbers. To understand why this rule exists, let’s consider an example. If you have -3 * 4, you’re essentially adding -3 together 4 times. This would be -3 + (-3) + (-3) + (-3) = -12. Therefore, -3 * 4 equals -12, demonstrating that the product of a negative and a positive number is negative.
| Operation | Result |
|---|---|
| -3 * 4 | -12 |
| -2 * 5 | -10 |
| -1 * 6 | -6 |

Key Points
- The product of a negative number and a positive number is always negative.
- Multiplication represents repeated addition, and when applied to negative numbers, it follows specific rules based on the signs of the numbers involved.
- Understanding these rules is crucial for performing arithmetic operations accurately and for solving mathematical problems that involve negative and positive numbers.
- Applying the rule for negative times positive helps in maintaining consistency and logic in mathematical calculations.
- It's essential to practice and reinforce the understanding of these concepts to improve mathematical proficiency.
Applications and Implications

The concept of negative times positive has numerous applications across various fields, including mathematics, physics, and engineering. In mathematics, understanding how to multiply negative and positive numbers is essential for solving equations and inequalities. In physics, negative numbers can represent directions or quantities that are opposite in nature, such as velocity or force. For instance, a negative velocity might indicate movement in the opposite direction of what’s considered positive.
Real-World Examples
A common real-world example of negative times positive can be seen in financial transactions. If you withdraw 100 from your account (considered a negative transaction because it reduces your balance), and you do this 5 times, the total reduction in your balance would be 500, which is a negative outcome. This scenario illustrates how multiplying a negative action (withdrawing money) by a positive number (the number of times the action is performed) results in a negative outcome.
Moreover, in the context of temperatures, if it's -5 degrees outside and this temperature is maintained for 3 consecutive days, the overall "coldness" or negative deviation from a baseline temperature (like 0 degrees) over these days can be seen as a product of the negative temperature and the positive number of days. This results in a greater negative deviation, highlighting the impact of sustained negative conditions over time.
Why is the product of a negative and a positive number always negative?
+This is because the operation of multiplying a negative number by a positive number essentially means adding a negative value a certain number of times, which always results in a negative outcome.
How does this concept apply to real-world scenarios?
+The concept applies in various scenarios, such as financial transactions, temperature changes, and physical movements, where the direction or nature of the quantity can be represented by negative or positive values.
What's the significance of understanding negative times positive in mathematics?
+Understanding this concept is crucial for performing accurate arithmetic operations, solving equations, and grasping more complex mathematical concepts that build upon these foundational principles.
In conclusion, the concept of negative times positive is a fundamental principle in mathematics that has wide-ranging implications and applications. By grasping this concept, individuals can better understand mathematical operations, solve problems more effectively, and apply these principles to real-world scenarios. The importance of this concept lies in its ability to provide a logical and consistent framework for dealing with negative and positive quantities, thereby facilitating a deeper understanding of mathematics and its applications.