Negative times negative is a fundamental concept in mathematics that can often lead to confusion, especially among students who are new to algebra and arithmetic operations. The idea that two negative numbers multiplied together result in a positive number seems counterintuitive at first glance. However, understanding the principle behind this operation is crucial for advancing in mathematics and appreciating the beauty of mathematical logic. In this article, we will delve into the concept of negative times negative, exploring its rationale, applications, and implications in various mathematical contexts.
Mathematical Rationale

The multiplication of two negative numbers resulting in a positive number is grounded in the basic principles of arithmetic and the definition of multiplication in the context of real numbers. When we multiply two numbers, we are essentially adding a number a certain number of times, equal to the multiplier. For example, 3 * 4 means adding 3 together 4 times (3 + 3 + 3 + 3 = 12). However, when we deal with negative numbers, we are considering the opposite direction or the additive inverse. Thus, multiplying a negative number by a positive number involves adding the additive inverse of the positive number a certain number of times, which results in a negative product.
Extension to Negative Times Negative
To understand why negative times negative equals positive, let’s consider the properties of multiplication and the concept of additive inverses. The additive inverse of a number is the value that, when added to the original number, results in zero. For example, the additive inverse of 5 is -5 because 5 + (-5) = 0. When we multiply two negative numbers, we are essentially dealing with the product of two additive inverses. The rationale is as follows: if we have -a * -b, we are asking how many times -a goes into -b. Considering -a as the additive inverse of a, and -b as the additive inverse of b, multiplying -a by -b essentially asks how many times the opposite of a goes into the opposite of b, which intuitively leads us back to the positive realm because we are, in a sense, canceling out the “negativity” by multiplying two opposites.
| Operation | Result | Explanation |
|---|---|---|
| Positive * Positive | Positive | Basic multiplication principle |
| Positive * Negative | Negative | Multiplying by the additive inverse |
| Negative * Positive | Negative | Symmetric property of multiplication |
| Negative * Negative | Positive | Multiplying two additive inverses |
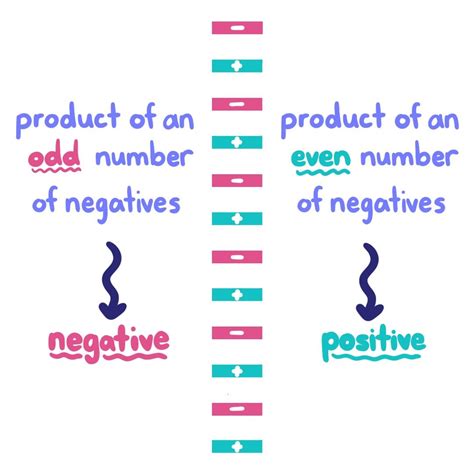
Applications and Implications

The concept of negative times negative has far-reaching implications across various branches of mathematics, including algebra, geometry, and calculus. In algebra, understanding this operation is crucial for solving quadratic equations and inequalities, which are fundamental tools for modeling real-world phenomena. In geometry, the concept is used to determine the orientation of shapes and vectors in space, which is critical in fields like physics and engineering. Furthermore, in calculus, the product rule for differentiation, which involves the multiplication of functions, relies on the understanding that negative times negative equals positive.
Real-World Applications
Beyond the theoretical framework, the concept of negative times negative has numerous practical applications. For instance, in economics, negative economic growth (a decrease in economic output) multiplied by a negative factor (such as a decrease in the rate of decrease) can result in a positive outcome (an increase in economic output), illustrating how understanding negative times negative can inform policy decisions. In physics, the concept is crucial for understanding the behavior of particles and forces, where directions and magnitudes are critical for predicting outcomes.
Key Points
- The multiplication of two negative numbers results in a positive number due to the properties of additive inverses and the definition of multiplication.
- Understanding this concept is crucial for advancing in mathematics and appreciating its internal logic and beauty.
- The concept has far-reaching implications across algebra, geometry, calculus, and various practical applications in economics, physics, and engineering.
- Real-world applications demonstrate the importance of grasping negative times negative for informed decision-making and problem-solving.
- The concept underscores the importance of foundational knowledge in mathematics for tackling complex problems and understanding the world around us.
In conclusion, the concept of negative times negative equals positive is a cornerstone of arithmetic and algebraic operations, with profound implications for mathematical structures and practical applications. By grasping this fundamental principle, individuals can deepen their understanding of mathematics, enhance their problem-solving abilities, and appreciate the intrinsic beauty and logic of mathematical concepts.
Why is negative times negative equal to positive?
+Negative times negative equals positive because when you multiply two negative numbers, you are essentially multiplying two additive inverses. This operation cancels out the “negativity,” leading to a positive result.
What are the practical applications of understanding negative times negative?
+Understanding negative times negative has practical applications in economics, physics, engineering, and other fields where mathematical modeling is used to predict outcomes and make informed decisions.
How does the concept of negative times negative relate to real-world phenomena?
+The concept relates to real-world phenomena by providing a mathematical framework for understanding and predicting changes in direction, magnitude, and orientation in various physical and economic systems.

