When it comes to understanding the rules of arithmetic operations, one of the most fundamental concepts to grasp is how to handle negative numbers. Negative numbers are an essential part of mathematics, representing quantities that are less than zero. Among the basic operations involving negative numbers, the multiplication of two negative numbers stands out, as it often leads to confusion among students and individuals not familiar with the underlying principles. The concept of multiplying two negative numbers is based on the rules of signs, which dictate that when you multiply two negative numbers together, the result is always positive.
Key Points
- The product of two negative numbers is always positive.
- This rule applies to all cases of multiplying two negative integers, fractions, or decimals.
- The reasoning behind this rule can be understood through the concept of additive inverses and the properties of multiplication.
- Understanding how to multiply negative numbers is crucial for solving equations, graphing functions, and performing various mathematical operations.
- Real-world applications of negative number multiplication can be seen in physics, engineering, and economics, where quantities such as temperatures, velocities, and financial losses are often represented by negative numbers.
The Mathematical Explanation

To delve into the mathematics behind the multiplication of negative numbers, let’s consider the basic principles of arithmetic. When we multiply two numbers, we are essentially adding a number a certain number of times. For instance, 3 multiplied by 4 is equivalent to adding 3 together 4 times (3 + 3 + 3 + 3 = 12). This concept can be extended to negative numbers by understanding that a negative number represents the opposite, or additive inverse, of a positive number. For example, -3 is the additive inverse of 3 because -3 + 3 = 0.
Applying the Rule of Signs
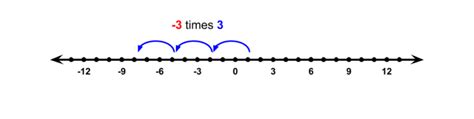
The rule of signs states that when multiplying two numbers with the same sign (either both positive or both negative), the result is positive. Conversely, when multiplying two numbers with different signs (one positive and one negative), the result is negative. This rule is based on the concept of directed numbers and how they represent quantities in different directions on the number line. For the specific case of multiplying two negative numbers, we apply this rule to get a positive result. For example, -3 multiplied by -4 equals 12, because both numbers have the same sign (negative), and thus their product is positive.
| Operation | Example | Result |
|---|---|---|
| Two negative numbers | -3 * -4 | 12 |
| Two positive numbers | 3 * 4 | 12 |
| One positive and one negative number | 3 * -4 | -12 |

Practical Applications
Beyond the theoretical framework, understanding how to multiply negative numbers has numerous practical applications. In physics, for instance, velocities and accelerations can be negative, indicating direction. The multiplication of these quantities to find distances or forces must accurately account for their signs. Similarly, in economics, financial losses can be represented by negative numbers, and calculating the total loss or the impact of certain economic policies may involve multiplying these negative quantities.
Education and Problem-Solving
In educational settings, grasping the concept of negative number multiplication is fundamental for advancing in mathematics and other STEM fields. It forms the basis for understanding more complex mathematical operations, such as solving quadratic equations and analyzing functions. Moreover, being able to apply this concept to real-world problems enhances problem-solving skills and fosters a deeper understanding of mathematical principles in action.
As we explore the vast expanse of mathematical concepts, the importance of understanding negative number multiplication becomes increasingly evident. It is not merely a rule to memorize but a foundational principle that underpins many mathematical and scientific applications. By delving into the reasoning behind this rule and exploring its applications, individuals can develop a more nuanced understanding of mathematics and its role in describing and analyzing the world around us.
Why is the product of two negative numbers positive?
+The product of two negative numbers is positive because of the rule of signs, which dictates that multiplying two numbers with the same sign yields a positive result. This rule is based on the concept of additive inverses and the properties of multiplication.
Can you provide an example of a real-world application of negative number multiplication?
+In physics, when calculating the work done by a force applied in the opposite direction of an object’s motion, you might multiply a negative force by a negative distance, resulting in a positive work done, which is a common application of negative number multiplication.
How does understanding negative number multiplication impact problem-solving skills in mathematics?
+Understanding negative number multiplication enhances problem-solving skills by providing a solid foundation for more complex mathematical operations. It allows individuals to approach problems with confidence, knowing how to handle negative quantities, and to apply mathematical principles accurately in a variety of contexts.



