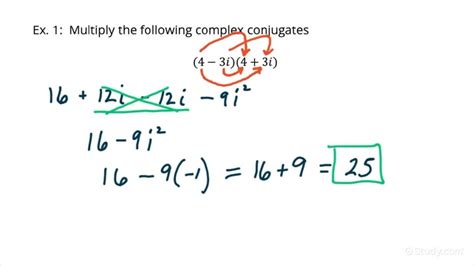Multiplying by conjugate is a fundamental concept in algebra, particularly in the context of rational expressions and complex numbers. This technique is used to simplify expressions and solve equations by eliminating radical terms or imaginary units. In essence, the conjugate of a binomial expression is another expression where the sign between the two terms is changed. For instance, the conjugate of $a + b$ is $a - b$, and the conjugate of $a - b$ is $a + b$. This concept is crucial in various mathematical operations, including multiplying, dividing, and simplifying complex expressions.
Understanding Conjugates in Algebra

In algebra, when we deal with expressions of the form a + \sqrt{b} or a + bi (where i is the imaginary unit), multiplying by the conjugate allows us to eliminate the radical or the imaginary part. The process involves multiplying both the numerator and the denominator by the conjugate of the denominator to rationalize the expression. This method is essential for simplifying expressions and making them more manageable in subsequent calculations. For example, the conjugate of 3 + 4i is 3 - 4i, and multiplying these two expressions gives us 9 + 12i - 12i - 16i^2. Since i^2 = -1, this simplifies to 9 + 16 = 25, which is a real number.
Multiplying by Conjugate in Complex Numbers
When dealing with complex numbers of the form a + bi, where a and b are real numbers and i is the imaginary unit, multiplying by the conjugate helps in simplifying expressions and finding the magnitude of complex numbers. The conjugate of a + bi is a - bi. Multiplying a complex number by its conjugate results in a real number, which is the square of the magnitude of the complex number. This property is widely used in algebra, geometry, and other branches of mathematics and physics. For instance, if we have a complex number z = 2 + 3i, its conjugate \bar{z} is 2 - 3i. Multiplying z by \bar{z} gives us (2 + 3i)(2 - 3i) = 4 - 6i + 6i - 9i^2 = 4 + 9 = 13.
| Complex Number | Conjugate | Product |
|---|---|---|
| $2 + 3i$ | $2 - 3i$ | $13$ |
| $4 - 5i$ | $4 + 5i$ | $41$ |

Key Points
- The conjugate of a binomial expression $a + b$ is $a - b$, and this concept is crucial for simplifying expressions in algebra and complex numbers.
- Multiplying by the conjugate is used to rationalize denominators and eliminate radical or imaginary terms, making expressions more manageable for further calculations.
- In complex numbers, multiplying a number by its conjugate yields a real number that represents the square of the magnitude of the complex number.
- This technique is fundamental in various mathematical and physical applications, including algebra, geometry, and physics, where complex numbers and their properties play a significant role.
- Understanding and applying the concept of conjugates and their multiplication is essential for solving equations, simplifying expressions, and interpreting geometric representations of complex numbers.
Applications and Implications

The concept of multiplying by conjugate has far-reaching implications in mathematics and physics. In electrical engineering, complex numbers are used to represent impedances and circuit analysis, where multiplying by conjugate helps in simplifying expressions and understanding circuit behavior. In physics, particularly in quantum mechanics, complex numbers are used to describe wave functions, and the concept of conjugate is essential for calculating probabilities and understanding the behavior of particles at the quantum level. Moreover, in signal processing and communication systems, complex numbers are used to represent signals, and the technique of multiplying by conjugate is crucial for filtering, modulation, and demodulation processes.
Real-World Examples and Analogies
To better understand the concept of multiplying by conjugate, it’s helpful to consider real-world analogies. For instance, in acoustics, when dealing with sound waves, complex numbers can represent the amplitude and phase of sound signals. Multiplying these signals by their conjugates can help in filtering out noise and understanding the characteristics of the sound. Similarly, in optics, complex numbers are used to describe the phase and amplitude of light waves, and the concept of conjugate is essential for understanding phenomena like interference and diffraction. These analogies highlight the practical significance of multiplying by conjugate in various fields of science and engineering.
What is the purpose of multiplying by conjugate in algebra and complex numbers?
+The primary purpose of multiplying by conjugate is to simplify expressions, eliminate radical or imaginary terms, and rationalize denominators, making it easier to perform subsequent calculations and understand the properties of complex numbers.
How does the concept of conjugate relate to the magnitude of complex numbers?
+Multiplying a complex number by its conjugate results in a real number that is the square of the magnitude of the complex number. This property is fundamental in understanding the geometric interpretation of complex numbers and their applications in physics and engineering.
What are some real-world applications of the concept of multiplying by conjugate?
+The concept of multiplying by conjugate has applications in electrical engineering, physics, signal processing, and communication systems. It is used for simplifying expressions, filtering signals, understanding circuit behavior, and describing wave functions in quantum mechanics.
In conclusion, the concept of multiplying by conjugate is a powerful tool in algebra and complex numbers, allowing for the simplification of expressions, elimination of radical or imaginary terms, and understanding of complex number properties. Its applications span across various fields of science and engineering, highlighting the importance of this technique in both theoretical and practical contexts. By grasping the concept of conjugates and their multiplication, individuals can deepen their understanding of complex numbers and their role in describing and analyzing phenomena in mathematics, physics, and engineering.