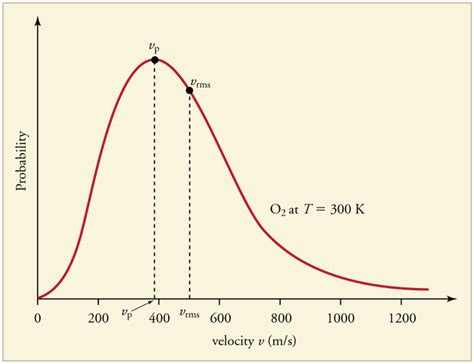
The Maxwell-Boltzmann distribution is a fundamental concept in statistical mechanics, describing the distribution of speeds among gas molecules in thermal equilibrium. This distribution is a cornerstone of kinetic theory, providing a mathematical framework for understanding the behavior of gases and their interactions with their surroundings. The distribution is named after James Clerk Maxwell and Ludwig Boltzmann, who independently developed the theory in the 19th century. In this article, we will delve into the intricacies of the Maxwell-Boltzmann distribution, exploring its underlying principles, mathematical formulation, and practical applications.
Historical Background and Development
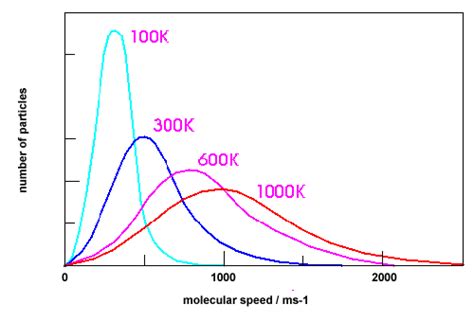
The Maxwell-Boltzmann distribution was first proposed by James Clerk Maxwell in 1860, as part of his work on the kinetic theory of gases. Maxwell’s initial formulation described the distribution of molecular speeds in a gas, assuming that the molecules were idealized, non-interacting particles. Later, in the 1870s, Ludwig Boltzmann expanded upon Maxwell’s work, introducing the concept of the “Boltzmann distribution” to describe the distribution of energies among molecules in a gas. The combined efforts of Maxwell and Boltzmann laid the foundation for the modern understanding of the Maxwell-Boltzmann distribution, which has since become a cornerstone of statistical mechanics.
Mathematical Formulation
The Maxwell-Boltzmann distribution is typically expressed as a probability density function, describing the probability that a molecule has a particular speed. The distribution is given by the equation:
f(v) = 4 \* π \* (m / 2 \* π \* k \* T)^(3/2) \* v^2 \* exp(-m \* v^2 / 2 \* k \* T)
where f(v) is the probability density function, v is the speed of the molecule, m is the mass of the molecule, k is the Boltzmann constant, and T is the temperature of the gas. This equation describes the distribution of speeds among gas molecules, with the probability of a molecule having a particular speed decreasing exponentially with increasing speed.
| Parameter | Description | Unit |
|---|---|---|
| m | Mass of the molecule | kg |
| k | Boltzmann constant | J/K |
| T | Temperature of the gas | K |
| v | Speed of the molecule | m/s |
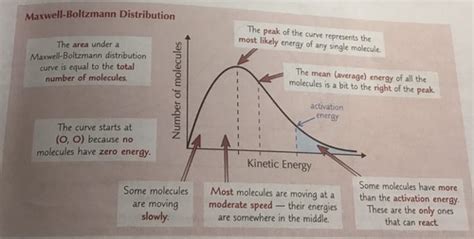
Key Applications and Implications
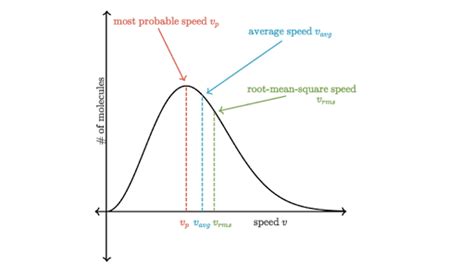
The Maxwell-Boltzmann distribution has numerous practical applications in various fields, including physics, chemistry, and engineering. Some of the key applications include:
- Gas Dynamics: The Maxwell-Boltzmann distribution is used to model the behavior of gases in various flow regimes, from laminar to turbulent flows.
- Thermodynamics: The distribution is used to derive the thermodynamic properties of gases, such as internal energy, enthalpy, and entropy.
- Chemical Kinetics: The Maxwell-Boltzmann distribution is used to model the rates of chemical reactions, taking into account the distribution of molecular speeds and energies.
Key Points
- The Maxwell-Boltzmann distribution describes the distribution of speeds among gas molecules in thermal equilibrium.
- The distribution is a cornerstone of kinetic theory, providing a mathematical framework for understanding gas behavior.
- The Maxwell-Boltzmann distribution has numerous practical applications in physics, chemistry, and engineering.
- The distribution is used to model the behavior of gases in various flow regimes, from laminar to turbulent flows.
- The Maxwell-Boltzmann distribution is used to derive the thermodynamic properties of gases, such as internal energy, enthalpy, and entropy.
Criticisms and Limitations
While the Maxwell-Boltzmann distribution is a powerful tool for understanding gas behavior, it is not without its limitations. Some of the criticisms and limitations of the distribution include:
The Maxwell-Boltzmann distribution assumes that the gas molecules are idealized, non-interacting particles, which is not always the case in real-world systems. Additionally, the distribution is based on a simplification of the underlying molecular dynamics, which can lead to inaccuracies in certain situations.
Despite these limitations, the Maxwell-Boltzmann distribution remains a fundamental concept in statistical mechanics, providing a mathematical framework for understanding the behavior of gases and their interactions with their surroundings.
What is the Maxwell-Boltzmann distribution used for?
+The Maxwell-Boltzmann distribution is used to model the behavior of gases in various flow regimes, from laminar to turbulent flows, and to derive the thermodynamic properties of gases, such as internal energy, enthalpy, and entropy.
What are the limitations of the Maxwell-Boltzmann distribution?
+The Maxwell-Boltzmann distribution assumes that the gas molecules are idealized, non-interacting particles, which is not always the case in real-world systems. Additionally, the distribution is based on a simplification of the underlying molecular dynamics, which can lead to inaccuracies in certain situations.
How is the Maxwell-Boltzmann distribution related to the ideal gas law?
+The Maxwell-Boltzmann distribution is related to the ideal gas law, as it provides a mathematical framework for understanding the behavior of gases and their interactions with their surroundings. The ideal gas law is a simplification of the Maxwell-Boltzmann distribution, which assumes that the gas molecules are idealized, non-interacting particles.
In conclusion, the Maxwell-Boltzmann distribution is a fundamental concept in statistical mechanics, describing the distribution of speeds among gas molecules in thermal equilibrium. The distribution has numerous practical applications in various fields, including physics, chemistry, and engineering, and provides a mathematical framework for understanding gas behavior and their interactions with their surroundings. While the distribution has its limitations, it remains a cornerstone of kinetic theory, and its implications continue to shape our understanding of the behavior of gases and their role in various natural and technological processes.