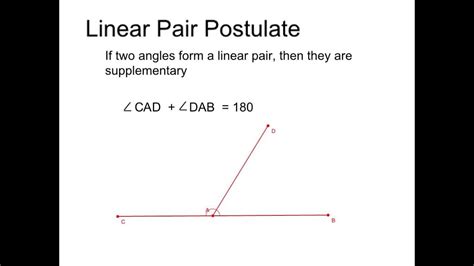
The Linear Pair Theorem is a fundamental concept in geometry, specifically in the study of angles and lines. It states that if two angles are adjacent to each other and form a straight line, then they are supplementary, meaning their sum is equal to 180 degrees. This theorem is crucial in various geometric proofs and calculations, particularly when dealing with angles, lines, and planes.
In more technical terms, the Linear Pair Theorem can be defined as: If two angles, ∠A and ∠B, are adjacent to each other and form a straight line, then ∠A + ∠B = 180°. This relationship holds true regardless of the orientation of the line or the position of the angles. The Linear Pair Theorem is a direct consequence of the definition of a straight line and the properties of angles formed when two lines intersect.
Key Points
- The Linear Pair Theorem applies to adjacent angles that form a straight line.
- Supplementary angles are angles whose sum is 180 degrees.
- The theorem is essential in geometric proofs involving angles and lines.
- It applies to all straight lines and adjacent angles, regardless of orientation or position.
- Understanding the Linear Pair Theorem is crucial for calculations involving angles in geometry.
Understanding the Linear Pair Theorem

The Linear Pair Theorem is straightforward yet powerful. It implies that any two angles that are adjacent to each other and form a straight line will always add up to 180 degrees. This is because a straight line is defined as 180 degrees, and when two angles together form this line, their sum must equal the total measure of the line. This concept is foundational in understanding more complex geometric principles and is used extensively in solving problems related to angles, triangles, and other geometric figures.
Applying the Linear Pair Theorem
The application of the Linear Pair Theorem is seen in various geometric problems. For instance, if one is given an angle and told that it forms a linear pair with another angle, one can immediately determine the measure of the second angle by subtracting the measure of the first angle from 180 degrees. This is particularly useful in solving for unknown angles in triangles, quadrilaterals, and other polygons, where knowing the measure of one angle can help in determining the measures of other angles through the application of the Linear Pair Theorem and other geometric principles.
| Angle Measure | Linear Pair Measure |
|---|---|
| 60° | 120° (since 180° - 60° = 120°) |
| 90° | 90° (since 180° - 90° = 90°) |
| 45° | 135° (since 180° - 45° = 135°) |

Extensions and Related Concepts

Beyond the Linear Pair Theorem, there are several related concepts in geometry that are worth exploring. These include the concept of supplementary angles, complementary angles, and the properties of vertical angles and corresponding angles. Understanding these concepts in conjunction with the Linear Pair Theorem provides a comprehensive foundation in geometry and enables the solution of complex problems with ease.
Supplementary and Complementary Angles
Supplementary angles, as mentioned, are angles whose sum is 180 degrees. Complementary angles, on the other hand, are angles whose sum is 90 degrees. These definitions are fundamental and are directly related to the Linear Pair Theorem. By understanding the relationships between different types of angles, one can apply geometric principles to solve problems in various fields, including design, construction, and physics.
In conclusion, the Linear Pair Theorem is a fundamental principle in geometry that has far-reaching implications for understanding and working with angles and lines. Its application is diverse, ranging from simple geometric problems to complex engineering designs. By grasping this theorem and its related concepts, one can develop a deep understanding of geometric principles and apply them in a variety of contexts.
What is the Linear Pair Theorem?
+The Linear Pair Theorem states that two angles that are adjacent to each other and form a straight line are supplementary, meaning their sum is 180 degrees.
How is the Linear Pair Theorem applied in geometry?
+The theorem is used to find the measure of an angle when it forms a linear pair with another angle of known measure. It is essential in solving problems related to angles in triangles, quadrilaterals, and other polygons.
What are supplementary angles?
+Supplementary angles are angles whose sum is 180 degrees. This concept is directly related to the Linear Pair Theorem, as angles forming a linear pair are always supplementary.