The inverse of the natural logarithm, denoted as ln^-1 or exp, is a fundamental concept in mathematics, particularly in calculus and algebra. It is defined as the inverse function of the natural logarithm, which is the logarithm to the base e, where e is approximately 2.71828. The natural logarithm function, ln(x), is the inverse of the exponential function, exp(x) = e^x. In other words, the inverse of ln(x) is exp(x), and vice versa.
Definition and Properties
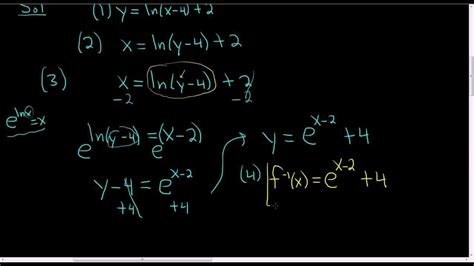
The inverse of the natural logarithm, exp(x), is defined as the function that satisfies the equation ln(exp(x)) = x for all real numbers x. This function can be expressed as exp(x) = e^x, where e is the base of the natural logarithm. The exponential function exp(x) has several important properties, including:
- It is a one-to-one function, meaning that each value of x corresponds to a unique value of exp(x).
- It is a continuous function, meaning that it can be drawn without lifting the pen from the paper.
- It is a differentiable function, meaning that it has a derivative at every point.
- It is an increasing function, meaning that as x increases, exp(x) also increases.
Mathematical Representation
The inverse of the natural logarithm can be represented mathematically as:
exp(x) = e^x = ∑n=0 to ∞
This representation is known as the Taylor series expansion of the exponential function, where n! denotes the factorial of n. The Taylor series expansion provides a way to approximate the value of exp(x) for any given x.
| Property | Description |
|---|---|
| Domain | All real numbers |
| Range | All positive real numbers |
| Derivative | exp(x) |
| Integral | e^x + C |
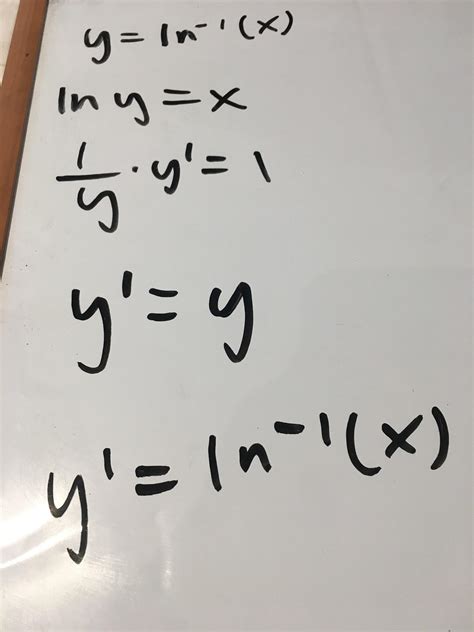
Key Points
- The inverse of the natural logarithm is denoted as ln^-1 or exp.
- It is defined as the inverse function of the natural logarithm, which is the logarithm to the base e.
- The exponential function exp(x) has several important properties, including being one-to-one, continuous, differentiable, and increasing.
- The inverse of the natural logarithm can be represented mathematically as exp(x) = e^x = ∑[n=0 to ∞] (x^n / n!).
- The Taylor series expansion provides a way to approximate the value of exp(x) for any given x.
Applications and Examples
The inverse of the natural logarithm has numerous applications in various fields, including science, engineering, and economics. Some examples include:
- Population growth: The exponential function can be used to model population growth, where the rate of growth is proportional to the current population.
- Compound interest: The exponential function can be used to calculate the future value of an investment, where the interest rate is compounded continuously.
- Chemical reactions: The exponential function can be used to model the rate of chemical reactions, where the rate of reaction is proportional to the concentration of reactants.
Real-World Examples
In real-world applications, the inverse of the natural logarithm is used to solve problems that involve exponential growth or decay. For example:
A company invests 10,000 in a savings account that earns an annual interest rate of 5%. The interest is compounded continuously, and the company wants to know the future value of the investment after 10 years. Using the exponential function, the future value can be calculated as:</p> <p>FV = PV \* e^(rt) = 10,000 * e^(0.05 * 10) ≈ $16,386.16
What is the domain of the inverse of the natural logarithm?
+The domain of the inverse of the natural logarithm is all real numbers.
What is the range of the inverse of the natural logarithm?
+The range of the inverse of the natural logarithm is all positive real numbers.
What is the derivative of the inverse of the natural logarithm?
+The derivative of the inverse of the natural logarithm is exp(x).
