The integrated rate law is a fundamental concept in chemical kinetics, describing the rate at which reactants are converted into products over time. For first-order reactions, the integrated rate law provides a straightforward way to analyze and predict the concentration of reactants and products as a function of time. In this article, we will delve into the details of the integrated rate law for first-order reactions, exploring its mathematical derivation, key features, and practical applications.
Mathematical Derivation of the Integrated Rate Law
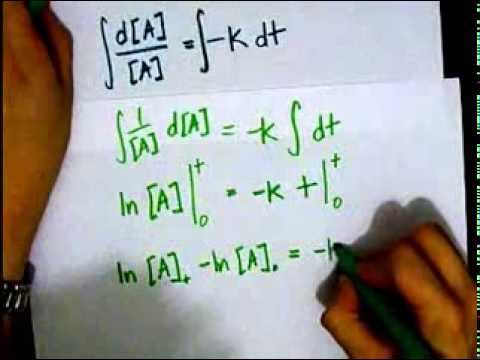
The integrated rate law for first-order reactions is derived from the differential rate law, which describes the rate of reaction as a function of the concentration of reactants. For a first-order reaction, the differential rate law is given by:
rate = k * [A]
where k is the rate constant, and [A] is the concentration of the reactant. To integrate this equation, we can separate the variables and integrate both sides:
∫(1/[A])d[A] = ∫kdt
Evaluating the integrals, we get:
ln([A]t/[A]0) = -kt
where [A]t is the concentration of the reactant at time t, [A]0 is the initial concentration, and k is the rate constant. This equation is the integrated rate law for first-order reactions.
Key Features of the Integrated Rate Law
The integrated rate law for first-order reactions has several key features that make it useful for analyzing and predicting the behavior of chemical reactions. Some of the most important features include:
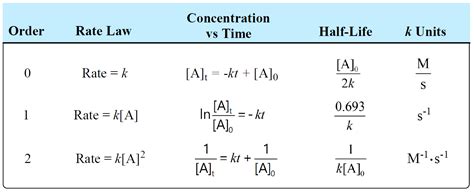
Linear Plot: When the integrated rate law is plotted as ln([A]t/[A]0) vs. time, the resulting graph is a straight line with a slope of -k. This provides a convenient way to determine the rate constant from experimental data.
Half-Life: The half-life of a first-order reaction is the time it takes for the concentration of the reactant to decrease by half. The half-life is related to the rate constant by the equation: t1/2 = ln(2)/k.
Concentration vs. Time: The integrated rate law can be rearranged to give the concentration of the reactant as a function of time: [A]t = [A]0 * e^(-kt). This equation provides a way to predict the concentration of the reactant at any given time.
| Rate Constant (k) | Half-Life (t1/2) |
|---|---|
| 0.1 min^(-1) | 6.93 min |
| 0.05 min^(-1) | 13.86 min |
| 0.01 min^(-1) | 69.31 min |

Key Points
- The integrated rate law for first-order reactions is given by the equation: ln([A]t/[A]0) = -kt.
- The half-life of a first-order reaction is related to the rate constant by the equation: t1/2 = ln(2)/k.
- The concentration of the reactant as a function of time can be predicted using the equation: [A]t = [A]0 \* e^(-kt).
- The integrated rate law can be used to determine the rate constant from experimental data by plotting ln([A]t/[A]0) vs. time.
- Understanding the integrated rate law is essential for designing and optimizing chemical reactions to achieve specific goals.
Practical Applications of the Integrated Rate Law
The integrated rate law for first-order reactions has a wide range of practical applications in chemistry and chemical engineering. Some of the most significant applications include:
Reaction Design: By understanding the integrated rate law, chemists and chemical engineers can design reactions to achieve specific goals, such as maximizing product yield or minimizing reaction time.
Process Optimization: The integrated rate law can be used to optimize reaction conditions, such as temperature and pressure, to achieve optimal reaction rates and yields.
Quality Control: The integrated rate law can be used to predict the concentration of reactants and products as a function of time, allowing for quality control and assurance in chemical manufacturing processes.
Real-World Examples
The integrated rate law for first-order reactions has numerous real-world applications. For example:
Pharmaceuticals: The integrated rate law is used to predict the degradation of pharmaceuticals over time, allowing for the development of stable formulations and packaging.
Food Processing: The integrated rate law is used to predict the spoilage of food products, allowing for the development of safe and effective preservation methods.
Environmental Remediation: The integrated rate law is used to predict the degradation of environmental pollutants, allowing for the development of effective remediation strategies.
What is the integrated rate law for first-order reactions?
+The integrated rate law for first-order reactions is given by the equation: ln([A]t/[A]0) = -kt.
How is the half-life of a first-order reaction related to the rate constant?
+The half-life of a first-order reaction is related to the rate constant by the equation: t1/2 = ln(2)/k.
What are some practical applications of the integrated rate law for first-order reactions?
+The integrated rate law has numerous practical applications, including reaction design, process optimization, quality control, and environmental remediation.
In conclusion, the integrated rate law for first-order reactions is a fundamental concept in chemical kinetics, providing a powerful tool for analyzing and predicting the behavior of chemical reactions. By understanding the key features and practical applications of this equation, chemists and chemical engineers can design and optimize reactions to achieve specific goals, such as maximizing product yield or minimizing reaction time. As we continue to develop and apply new technologies and processes, the integrated rate law will remain an essential tool for advancing our understanding of chemical reactions and their role in shaping our world.



