Absolute value equations are a fundamental concept in mathematics, and solving them is crucial for various applications in algebra, geometry, and other fields. The absolute value of a number is its distance from zero on the number line, without considering direction. In this article, we will delve into the world of absolute value equations, exploring the concepts, methods, and techniques for solving them. Whether you're a student, teacher, or simply a math enthusiast, this comprehensive guide will provide you with a deep understanding of how to tackle absolute value equations with confidence.
Key Points
- Understanding the definition and properties of absolute value
- Learning to solve basic absolute value equations
- Applying algebraic techniques to solve complex absolute value equations
- Handling equations with multiple absolute value terms
- Practicing with examples to reinforce problem-solving skills
Introduction to Absolute Value Equations
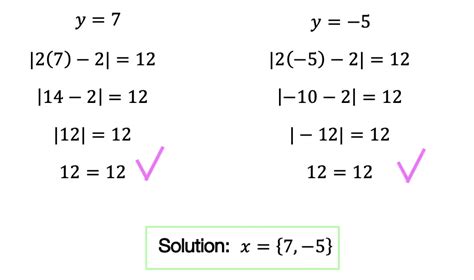
Absolute value equations involve the absolute value of a variable or expression, which is denoted by two vertical lines, | |. The general form of an absolute value equation is |x| = a, where x is the variable and a is a constant. To solve an absolute value equation, we need to find the values of x that satisfy the equation. The key concept here is that the absolute value of a number can be either positive or negative, but its distance from zero remains the same.
Basic Absolute Value Equations
Let’s start with a simple example: |x| = 5. To solve this equation, we need to find the values of x that are 5 units away from zero on the number line. There are two such values: x = 5 and x = -5. Therefore, the solutions to the equation are x = 5 and x = -5.
In general, if |x| = a, then x = a and x = -a are the solutions to the equation. This is because the absolute value of a number is its distance from zero, and there are two numbers that are a units away from zero: a and -a.
Solving Absolute Value Equations with Variables

Now, let’s consider a more complex example: |2x - 3| = 7. To solve this equation, we need to isolate the variable x. We can start by rewriting the equation as 2x - 3 = 7 or 2x - 3 = -7, since the absolute value of 2x - 3 is 7.
Solving the first equation, we get 2x = 10, which implies x = 5. Solving the second equation, we get 2x = -4, which implies x = -2. Therefore, the solutions to the equation are x = 5 and x = -2.
Algebraic Techniques for Solving Absolute Value Equations
When solving absolute value equations, it’s essential to use algebraic techniques to isolate the variable. We can use addition, subtraction, multiplication, and division to simplify the equation and solve for the variable. However, we need to be careful when working with absolute value equations, as the variable can take on both positive and negative values.
For example, consider the equation |x + 2| = 3. To solve this equation, we can rewrite it as x + 2 = 3 or x + 2 = -3. Solving the first equation, we get x = 1. Solving the second equation, we get x = -5. Therefore, the solutions to the equation are x = 1 and x = -5.
| Equation | Solutions |
|---|---|
| |x| = 5 | x = 5, x = -5 |
| |2x - 3| = 7 | x = 5, x = -2 |
| |x + 2| = 3 | x = 1, x = -5 |

Handling Equations with Multiple Absolute Value Terms
Sometimes, we encounter equations with multiple absolute value terms. For example, consider the equation |x + 2| + |x - 3| = 5. To solve this equation, we need to consider different cases based on the signs of the expressions x + 2 and x - 3.
Case 1: x + 2 ≥ 0 and x - 3 ≥ 0. In this case, the equation becomes x + 2 + x - 3 = 5, which simplifies to 2x - 1 = 5. Solving for x, we get x = 3.
Case 2: x + 2 ≥ 0 and x - 3 < 0. In this case, the equation becomes x + 2 - (x - 3) = 5, which simplifies to 5 = 5. This is a true statement, and we can see that x = 1 is a solution to the equation.
Case 3: x + 2 < 0 and x - 3 ≥ 0. This case is not possible, since x cannot be both less than -2 and greater than or equal to 3.
Case 4: x + 2 < 0 and x - 3 < 0. In this case, the equation becomes - (x + 2) - (x - 3) = 5, which simplifies to -2x + 1 = 5. Solving for x, we get x = -2.
Therefore, the solutions to the equation are x = 3, x = 1, and x = -2.
Conclusion and Final Thoughts
In conclusion, solving absolute value equations requires a deep understanding of the concept of absolute value and the ability to apply algebraic techniques to isolate the variable. By considering both positive and negative solutions and using case analysis, we can solve even the most complex absolute value equations. Remember to always check your solutions to ensure that they satisfy the original equation, and don’t be afraid to ask for help if you’re struggling with a particular problem.
What is the definition of absolute value?
+The absolute value of a number is its distance from zero on the number line, without considering direction.
How do I solve a basic absolute value equation?
+To solve a basic absolute value equation, we need to find the values of x that are a units away from zero on the number line. For example, if |x| = 5, then x = 5 and x = -5 are the solutions to the equation.
What is the difference between an absolute value equation and a linear equation?
+An absolute value equation involves the absolute value of a variable or expression, whereas a linear equation is a polynomial equation of degree one. Absolute value equations can have multiple solutions, whereas linear equations typically have only one solution.
Meta Description: Learn how to solve absolute value equations with our comprehensive guide. Discover the concepts, methods, and techniques for solving absolute value equations, and practice with examples to reinforce your problem-solving skills.



