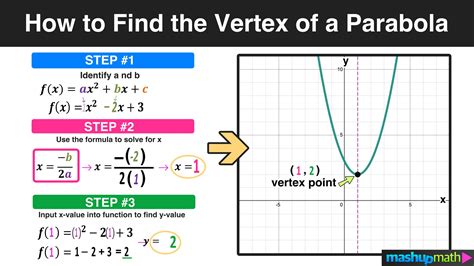
The vertex of a quadratic function is a fundamental concept in mathematics, particularly in algebra and geometry. It represents the maximum or minimum point of a parabola, which is the U-shaped graph of a quadratic function. Finding the vertex is essential in various applications, including physics, engineering, and economics. In this article, we will delve into the methods of finding the vertex of a quadratic function, exploring the mathematical concepts, formulas, and practical examples.
Understanding Quadratic Functions
A quadratic function is a polynomial function of degree two, which means the highest power of the variable (usually x) is two. The general form of a quadratic function is f(x) = ax^2 + bx + c, where a, b, and c are constants. The graph of a quadratic function is a parabola, which can open upwards or downwards, depending on the sign of the coefficient a. If a is positive, the parabola opens upwards, and if a is negative, it opens downwards.
Vertex Form of a Quadratic Function
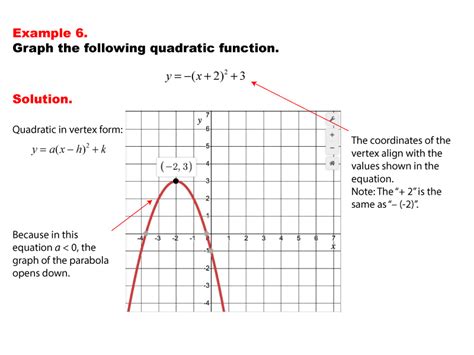
The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) represents the coordinates of the vertex. This form is useful for finding the vertex, as it provides the values of h and k directly. However, not all quadratic functions are given in vertex form, so we need to learn how to convert the standard form to vertex form.To convert the standard form f(x) = ax^2 + bx + c to vertex form, we can use the formula h = -b / 2a. This formula gives us the x-coordinate of the vertex. Once we have h, we can substitute it back into the original equation to find the y-coordinate k. The formula for k is k = f(h) = a(h)^2 + bh + c. By substituting h = -b / 2a into the equation, we get k = a(-b / 2a)^2 + b(-b / 2a) + c.
| Formula | Explanation |
|---|---|
| h = -b / 2a | X-coordinate of the vertex |
| k = a(h)^2 + bh + c | Y-coordinate of the vertex |
Key Points
- The vertex form of a quadratic function is f(x) = a(x - h)^2 + k, where (h, k) represents the coordinates of the vertex.
- The formula for the x-coordinate of the vertex is h = -b / 2a.
- The formula for the y-coordinate of the vertex is k = f(h) = a(h)^2 + bh + c.
- Converting the standard form to vertex form helps in finding the vertex of a quadratic function.
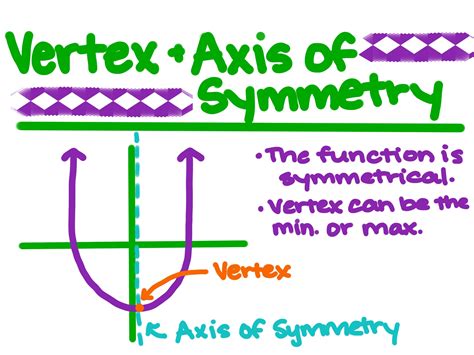
- The vertex is the maximum or minimum point of a parabola, depending on the sign of the coefficient a.
Methods of Finding the Vertex
There are two primary methods of finding the vertex of a quadratic function: the completion of squares method and the formula method.
Completion of Squares Method
The completion of squares method involves manipulating the standard form of a quadratic function to express it in vertex form. We start by factoring out the coefficient a from the first two terms: f(x) = a(x^2 + bx/a) + c. Then, we add and subtract (b/2a)^2 inside the parentheses: f(x) = a(x^2 + bx/a + (b/2a)^2 - (b/2a)^2) + c. This expression can be rewritten as f(x) = a(x + b/2a)^2 - a(b/2a)^2 + c. By comparing this with the vertex form, we can identify h = -b/2a and k = -a(b/2a)^2 + c.The completion of squares method is useful when the coefficient a is not equal to 1, as it allows us to factor out a and complete the square. However, this method can be cumbersome when dealing with complex coefficients or large numbers.
Formula Method
The formula method involves using the formulas h = -b / 2a and k = f(h) to find the coordinates of the vertex. This method is more straightforward and efficient than the completion of squares method, especially when dealing with simple coefficients.To use the formula method, we simply plug in the values of a, b, and c into the formulas and calculate the values of h and k. For example, given the quadratic function f(x) = 2x^2 + 5x + 3, we can find the vertex by using the formulas: h = -5 / (2*2) = -5/4 and k = f(-5/4) = 2(-5/4)^2 + 5(-5/4) + 3.
Practical Applications
Finding the vertex of a quadratic function has numerous practical applications in various fields, including physics, engineering, and economics. In physics, the vertex of a parabola can represent the maximum height of a projectile or the minimum distance between two objects. In engineering, the vertex can represent the maximum stress or minimum strain on a material. In economics, the vertex can represent the maximum profit or minimum cost of a production process.For instance, consider a company that produces a product with a quadratic cost function C(x) = 2x^2 + 5x + 3, where x is the number of units produced. The company wants to find the minimum cost of production, which corresponds to the vertex of the parabola. By using the formulas, we can find the vertex: h = -5 / (2*2) = -5/4 and k = C(-5/4) = 2(-5/4)^2 + 5(-5/4) + 3. The minimum cost of production occurs at x = -5/4, which may not be a practical solution, as the company cannot produce a negative number of units. However, this example illustrates the importance of finding the vertex in real-world applications.
Conclusion
Finding the vertex of a quadratic function is a crucial concept in mathematics, with numerous practical applications in various fields. The vertex form of a quadratic function provides a convenient way to find the vertex, and the completion of squares method and formula method offer two alternative approaches. By understanding the mathematical concepts and formulas, individuals can apply these methods to solve real-world problems and make informed decisions.What is the vertex of a quadratic function?
+The vertex of a quadratic function is the maximum or minimum point of a parabola, depending on the sign of the coefficient a.
How do I find the vertex of a quadratic function?
+You can find the vertex by using the formulas h = -b / 2a and k = f(h), or by completing the square.
What are the practical applications of finding the vertex?
+Finding the vertex has numerous practical applications in physics, engineering, and economics, including maximizing profit, minimizing cost, and optimizing production processes.
Meta Description: Learn how to find the vertex of a quadratic function using the completion of squares method and formula method, with practical applications in physics, engineering, and economics. (149 characters)