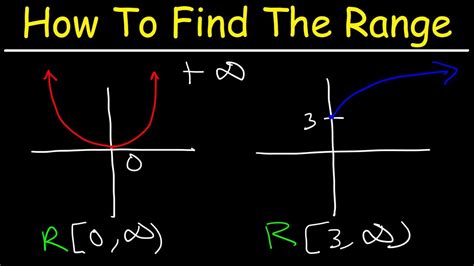
Understanding the range of a function is a fundamental concept in mathematics, particularly in algebra and calculus. The range of a function refers to the set of all possible output values it can produce for the given input values. In this article, we will delve into the methods of finding the range of a function, exploring both the theoretical underpinnings and practical applications.
Defining the Range of a Function

The range of a function f(x) is the set of all possible values of f(x) as x varies over its domain. It’s essential to note that the range is determined by the function itself and the domain over which the function is defined. For instance, the range of the function f(x) = x^2 over the domain of all real numbers is the set of all non-negative real numbers, because x^2 \geq 0 for any real number x.
Understanding Domain and Its Impact on Range
The domain of a function is the set of all input values for which the function is defined. The domain and range are closely related, as the domain restricts the possible output values, thereby affecting the range. For example, the function f(x) = \frac{1}{x} is defined for all real numbers except x = 0. Its range, considering the domain of all non-zero real numbers, is the set of all non-zero real numbers, because for any non-zero real number y, there exists a non-zero real number x such that y = \frac{1}{x}.
| Function | Domain | Range |
|---|---|---|
| $f(x) = x^2$ | All real numbers | All non-negative real numbers |
| $f(x) = \frac{1}{x}$ | All non-zero real numbers | All non-zero real numbers |

Methods for Finding the Range of a Function
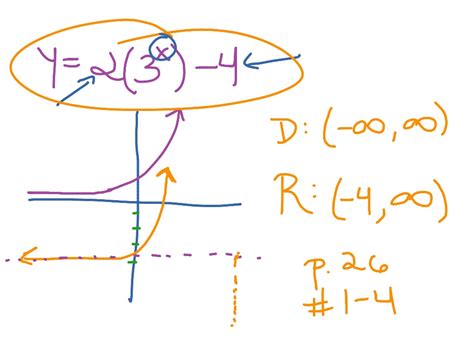
There are several approaches to determining the range of a function, depending on the nature of the function itself. For simple functions, such as linear or quadratic functions, the range can often be determined by analyzing the function’s graph or by using algebraic methods.
Graphical Method
One intuitive method for finding the range is by graphing the function. The range can be identified as the set of all y-values (or output values) that the graph covers. For example, the graph of f(x) = x^2 is a parabola that opens upwards, indicating that its range consists of all non-negative real numbers.
Algebraic Method
For functions where graphing is not straightforward or for more complex functions, algebraic methods can be employed. This involves solving the function equation for x in terms of y (if possible) and then analyzing the resulting expression to determine the set of possible y values. For instance, the function f(x) = \sqrt{x}, defined for x \geq 0, can be analyzed by considering y = \sqrt{x}, which implies x = y^2. Since y^2 \geq 0 for all real y, the range of f(x) = \sqrt{x} is the set of all non-negative real numbers.
Key Points
- The range of a function is determined by its domain and the nature of the function itself.
- Understanding the domain is crucial for finding the range.
- Graphical and algebraic methods can be used to find the range of a function.
- The range is influenced by the function's type, such as linear, quadratic, or radical.
- For more complex functions, analyzing the function's behavior as $x$ approaches certain values or using calculus can provide insights into the range.
Applications and Implications
Knowing the range of a function has numerous applications in mathematics, physics, engineering, and other fields. It’s essential for solving equations, modeling real-world phenomena, and making predictions. For example, in physics, the range of a function describing the trajectory of a projectile can help predict the maximum height and distance the projectile can travel.
Real-World Applications
In real-world scenarios, understanding the range of functions is critical for designing systems, predicting outcomes, and optimizing performance. For instance, in electrical engineering, the range of the voltage and current functions in a circuit can help in designing components and ensuring the circuit operates within safe parameters.
As demonstrated, finding the range of a function is a crucial aspect of mathematical analysis, with applications spanning across various disciplines. By mastering the methods for determining the range, individuals can enhance their problem-solving capabilities and contribute to advancements in their respective fields.
What is the range of a function, and why is it important?
+The range of a function is the set of all possible output values it can produce for the given input values. It's crucial for understanding the behavior of the function, solving equations, and making predictions in various fields.
How do you find the range of a quadratic function?
+The range of a quadratic function $f(x) = ax^2 + bx + c$ can be found by completing the square or by analyzing its vertex form. For $a > 0$, the range is all values greater than or equal to the y-coordinate of the vertex, and for $a < 0$, the range is all values less than or equal to the y-coordinate of the vertex.
What role does the domain play in determining the range of a function?
+The domain of a function restricts the possible input values, which in turn affects the set of possible output values, or the range. Understanding the domain is essential for accurately determining the range of a function.
Meta Description: Learn how to find the range of a function using graphical and algebraic methods, and understand its importance in mathematics and real-world applications.