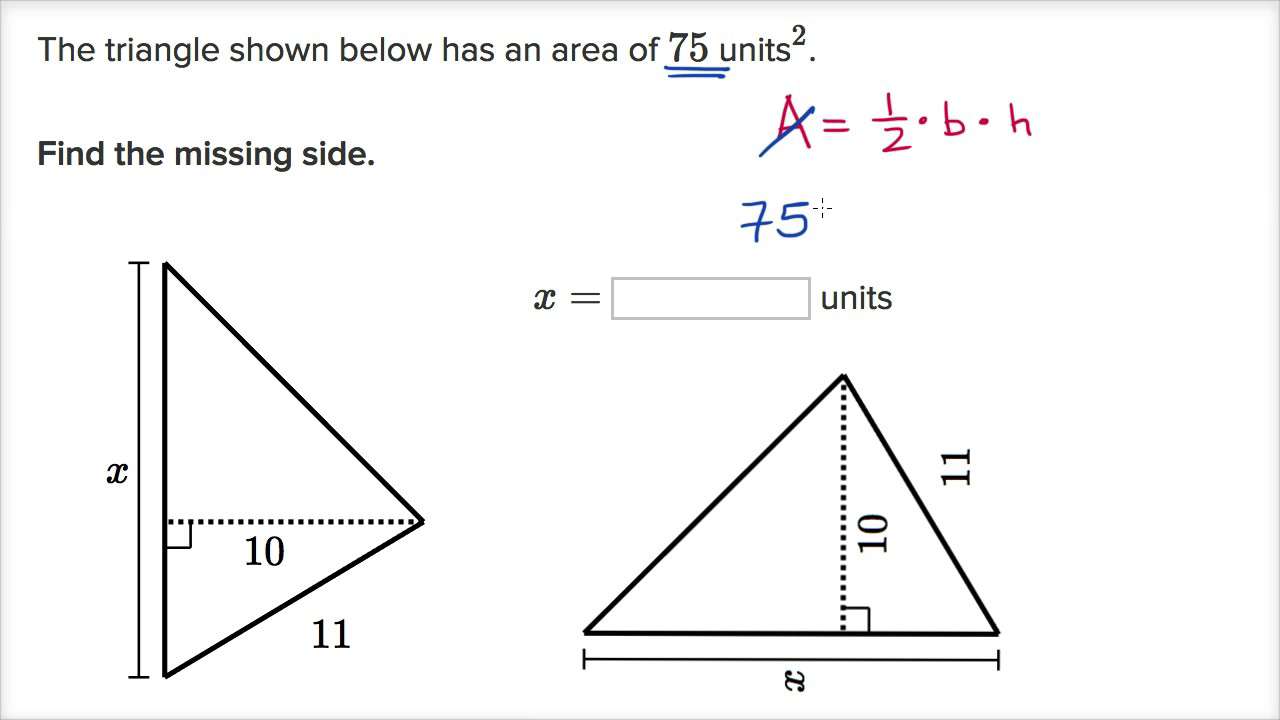
When dealing with triangles, one of the most fundamental concepts is the relationship between the lengths of their sides. Finding the missing side of a triangle can be crucial in various mathematical and real-world applications, such as architecture, engineering, and physics. The process of determining the missing side involves understanding the properties of triangles and applying relevant geometric principles. In this article, we will delve into the methods for finding the missing side of a triangle, exploring both basic and advanced techniques.
Key Points
- Understanding the types of triangles and their properties is essential for finding the missing side.
- The Pythagorean theorem is a fundamental tool for right-angled triangles.
- Trigonometric ratios can be used in both right-angled and non-right-angled triangles.
- The Law of Cosines is particularly useful for finding the missing side in non-right-angled triangles when all angles and one side are known.
- Applying geometric principles and theorems can simplify the process of finding the missing side.
Types of Triangles and Basic Properties
Triangles can be classified into several types based on their sides and angles. The most common types include equilateral (all sides are equal), isosceles (two sides are equal), and scalene (all sides are unequal) triangles. Additionally, triangles can be right-angled (one angle is 90 degrees), obtuse-angled (one angle is greater than 90 degrees), or acute-angled (all angles are less than 90 degrees). Understanding the type of triangle you are dealing with can significantly simplify the process of finding the missing side.
Pythagorean Theorem for Right-Angled Triangles
The Pythagorean theorem is a fundamental principle in geometry that states in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. Mathematically, this can be expressed as (c^2 = a^2 + b^2), where (c) is the length of the hypotenuse, and (a) and (b) are the lengths of the other two sides. This theorem is widely used for finding the missing side in right-angled triangles.
| Triangle Type | Formula | Description |
|---|---|---|
| Right-Angled | c^2 = a^2 + b^2 | Pythagorean theorem for finding the hypotenuse or a side. |

Trigonometric Ratios for Finding Missing Sides

Trigonometric ratios, including sine, cosine, and tangent, are essential for finding the missing sides in both right-angled and non-right-angled triangles. These ratios relate the angles of a triangle to the ratios of the lengths of its sides. For instance, in a right-angled triangle, the sine of an angle is defined as the ratio of the length of the side opposite the angle to the length of the hypotenuse, the cosine is the ratio of the length of the side adjacent to the angle to the length of the hypotenuse, and the tangent is the ratio of the length of the side opposite the angle to the length of the side adjacent to the angle.
Law of Cosines for Non-Right-Angled Triangles
The Law of Cosines is an extension of the Pythagorean theorem and is used for finding the missing side in non-right-angled triangles when all angles and one side are known. The formula for the Law of Cosines is (c^2 = a^2 + b^2 - 2ab\cos©), where (c) is the unknown side, (a) and (b) are the known sides, and (C) is the angle opposite side (c). This law provides a powerful tool for solving triangles in various contexts.
Applying Geometric Principles
Beyond the specific formulas and theorems, understanding and applying geometric principles can significantly aid in finding the missing side of a triangle. This includes recognizing properties such as congruence, similarity, and the relationships between angles and sides. For instance, if two triangles are similar, the ratio of the lengths of their corresponding sides is equal. This principle can be used to find missing sides by setting up proportions.
In conclusion, finding the missing side of a triangle involves a combination of understanding the properties of triangles, applying relevant geometric principles, and using specific formulas and theorems. Whether dealing with right-angled triangles and the Pythagorean theorem or non-right-angled triangles and the Law of Cosines, having a solid grasp of these concepts is essential for solving a wide range of problems in geometry and real-world applications.
What is the most straightforward method for finding the missing side in a right-angled triangle?
+The Pythagorean theorem is the most straightforward method, given by (c^2 = a^2 + b^2), where (c) is the length of the hypotenuse, and (a) and (b) are the lengths of the other two sides.
Can the Law of Cosines be used for right-angled triangles?
+Yes, the Law of Cosines can be used for right-angled triangles. However, it simplifies to the Pythagorean theorem when the angle (C = 90) degrees, because (\cos(90^\circ) = 0), resulting in (c^2 = a^2 + b^2).
What is the role of trigonometric ratios in finding the missing side of a triangle?
+Trigonometric ratios (sine, cosine, and tangent) are used to find the missing side in triangles, especially when dealing with right-angled triangles. They relate the angles of a triangle to the ratios of the lengths of its sides.