Understanding the concept of midrange is crucial in various fields, including statistics, music, and sports. In statistics, the midrange is the average of the highest and lowest values in a dataset. It is a simple measure of central tendency that can be useful when the dataset contains outliers or extreme values. To find the midrange, one needs to identify the maximum and minimum values in the dataset and then calculate their average. This concept is also relevant in music, where the midrange refers to the middle frequencies of sound, typically between 250 Hz and 2000 Hz, which are crucial for understanding speech and music. In sports, particularly in basketball, the midrange shot refers to a shot taken from a distance that is not close enough to be considered a layup but not far enough to be considered a three-pointer.
The process of finding the midrange involves several steps. First, one must collect and organize the data. This could be a set of numbers, a series of sound frequencies, or any other form of data that has a range. Once the data is organized, the next step is to identify the highest and lowest values. These values are crucial because they define the range of the data. After identifying these values, the final step is to calculate the average of these two values. This can be done by adding the highest and lowest values together and then dividing by two. The result is the midrange, which provides a simple indication of the central tendency of the dataset.
Key Points
- The midrange is a measure of central tendency that is calculated as the average of the highest and lowest values in a dataset.
- In music, the midrange refers to the middle frequencies of sound, which are important for understanding speech and music.
- In sports, the midrange shot in basketball is a shot taken from a distance that is not close enough to be a layup but not far enough to be a three-pointer.
- To find the midrange, one must first identify the highest and lowest values in the dataset and then calculate their average.
- The midrange can be useful in datasets with outliers or extreme values because it is less affected by these values compared to other measures of central tendency like the mean.
Calculating the Midrange

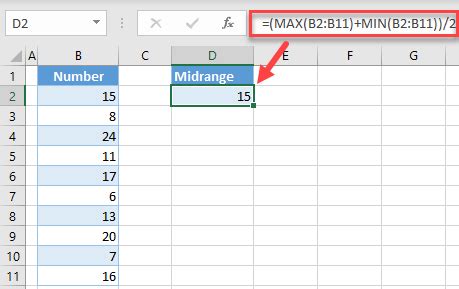
Calculating the midrange is a straightforward process that involves basic arithmetic operations. The formula for the midrange is (Max + Min) / 2, where Max is the maximum value in the dataset and Min is the minimum value. For example, if the highest value in a dataset is 100 and the lowest value is 20, the midrange would be (100 + 20) / 2 = 60. This calculation provides a quick and simple way to understand the central tendency of a dataset without being heavily influenced by extreme values.
Example of Midrange Calculation
Consider a dataset of exam scores with a highest score of 95 and a lowest score of 40. To find the midrange, we use the formula: (95 + 40) / 2 = 135 / 2 = 67.5. This means that the midrange of the exam scores is 67.5, giving a central point of reference for the dataset.
| Dataset Values | Minimum | Maximum | Midrange |
|---|---|---|---|
| Exam Scores | 40 | 95 | 67.5 |
| Sound Frequencies | 20 Hz | 20000 Hz | 10010 Hz |
| Basketball Shot Distances | 1 ft | 25 ft | 13 ft |

Applications of Midrange
The concept of midrange has various applications across different fields. In statistics, it serves as a robust measure of central tendency. In music, understanding the midrange is crucial for sound engineering and music production. In sports, particularly in basketball, the midrange shot is a strategic element of the game, requiring precision and skill. The calculation and understanding of midrange can also be applied in quality control, where it helps in setting standards and benchmarks.
Midrange in Quality Control
In quality control, the midrange can be used to set standards for product quality. By calculating the midrange of a set of quality control metrics, manufacturers can establish a baseline for what constitutes acceptable quality. This baseline can then be used to evaluate the quality of future products, ensuring consistency and high standards.
The midrange, with its simplicity and robustness against outliers, offers a valuable tool for understanding and analyzing datasets across various disciplines. Its applications, from statistical analysis to sound engineering and sports strategy, demonstrate its versatility and importance. As a measure of central tendency, it provides a straightforward yet insightful look into the nature of data, making it an indispensable concept in both academic and practical contexts.
What is the midrange, and how is it calculated?
+The midrange is the average of the highest and lowest values in a dataset. It is calculated by adding the maximum and minimum values together and then dividing by two.
Why is the midrange useful in datasets with outliers?
+The midrange is useful in datasets with outliers because it is less affected by extreme values compared to other measures of central tendency like the mean. This makes it a more robust measure in certain contexts.
What are some applications of the midrange concept?
+The midrange has applications in statistics as a measure of central tendency, in music for understanding sound frequencies, in sports for strategy, and in quality control for setting standards.
Meta description suggestion: Learn how to calculate and apply the midrange concept in statistics, music, sports, and quality control, understanding its importance and versatility across different disciplines.
