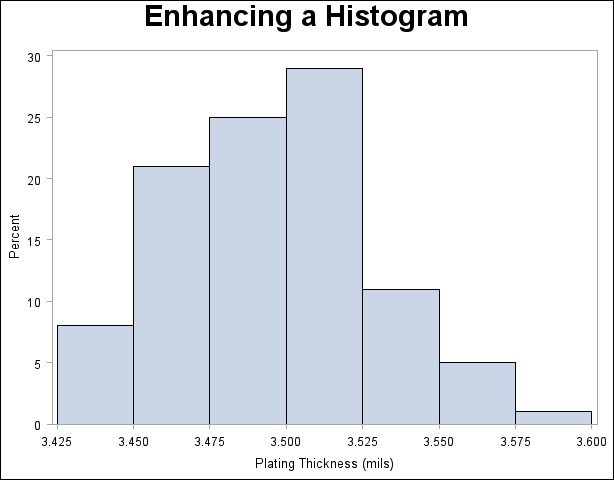
Constructing a histogram is a fundamental skill in data analysis and visualization, allowing us to represent the distribution of a dataset in a clear and concise manner. A histogram is a graphical representation that organizes a group of data points into specified ranges, displaying the frequency or density of data points within each range. This tool is invaluable for understanding the distribution of data, identifying patterns, and making informed decisions based on data insights. In this article, we will delve into the step-by-step process of constructing a histogram, exploring its components, and discussing best practices for effective data visualization.
Key Points
- Define the purpose and scope of the histogram to ensure it meets the analytical needs.
- Determine the bin size and range to effectively display the data distribution.
- Choose appropriate labels and titles for clarity and context.
- Consider the color scheme and visual elements to enhance readability and interpretation.
- Interpret the histogram by analyzing the shape, central tendency, and variability of the data.
Step-by-Step Construction of a Histogram
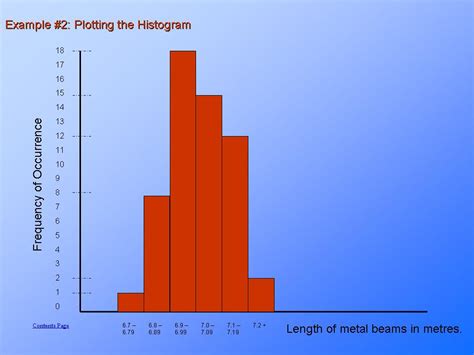
To construct a histogram, follow these steps:
1. Data Collection: Gather the data you wish to analyze. Ensure it is quantitative and suitable for histogram representation.
2. Determine the Bin Size and Range: Decide on the number of bins (or intervals) and the range of values each bin will cover. The choice of bin size affects the histogram’s appearance and interpretability. A common rule of thumb is to use the square root of the number of data points as the number of bins, but this can be adjusted based on the data’s characteristics and the purpose of the analysis.
3. Assign Data Points to Bins: Sort the data into the predetermined bins. Each data point falls into one bin based on its value.
4. Count the Frequency of Each Bin: Calculate how many data points are in each bin. This frequency represents the height of each bar in the histogram.
5. Plot the Histogram: Draw the histogram with bars representing the bins and their heights corresponding to the frequencies. The x-axis represents the value range of the bins, and the y-axis represents the frequency or density.
Interpreting Histograms
Once a histogram is constructed, interpreting it is crucial for extracting meaningful insights from the data. Key aspects to consider include:
- Shape: The overall shape of the histogram can indicate if the data follows a normal distribution, is skewed, or has multiple peaks.
- Central Tendency: The histogram can help identify the central tendency of the data, such as the mean, median, or mode, based on the distribution’s peak and symmetry.
- Variability: The spread of the data can be observed, indicating how much individual data points deviate from the central tendency.
- Outliers: Data points that fall far outside the main distribution can be identified as potential outliers, which may require further investigation.
| Bin Range | Frequency |
|---|---|
| 0-10 | 10 |
| 11-20 | 20 |
| 21-30 | 30 |
| 31-40 | 15 |
| 41-50 | 5 |
Best Practices for Histogram Construction
Effective histogram construction requires attention to several best practices to ensure clarity, accuracy, and meaningful interpretation:
- Clear Labels and Titles: Use descriptive labels for the axes and a title that clearly states the subject of the histogram.
- Appropriate Bin Size: The bin size should be chosen to reveal the underlying distribution without obscuring important details.
- Color Scheme: For histograms with multiple datasets, use distinct colors to differentiate between them, ensuring the colors are accessible to color-blind readers.
- Consistency: Maintain consistency in formatting and style, especially when comparing multiple histograms.
Advanced Considerations
In addition to the basic construction and interpretation of histograms, there are advanced considerations that can enhance the analysis and visualization:
- Density Plots: Instead of frequencies, histograms can be constructed to show density, which is particularly useful for comparing distributions with different bin widths.
- Cumulative Histograms: Showing the cumulative frequency or percentage can help in understanding the proportion of data points below a certain value.
- Interactive Visualizations: Utilizing interactive tools can allow for dynamic adjustment of bin sizes, zooming, and hovering over bins for detailed information, enhancing the exploratory data analysis experience.
What is the primary difference between a histogram and a bar chart?
+A histogram is used for continuous data and shows the distribution of data, whereas a bar chart is used for categorical data and compares different groups.
How do I choose the optimal bin size for my histogram?
+The choice of bin size depends on the number of data points and the desired level of detail. A common approach is to use the square root of the number of data points as the number of bins, but this can be adjusted based on the specific characteristics of the data and the purpose of the analysis.
Can histograms be used for non-numerical data?
+Histograms are specifically designed for numerical data. For non-numerical or categorical data, other types of charts such as bar charts or pie charts are more appropriate.
In conclusion, constructing a histogram is a systematic process that involves defining the data range, determining the bin size, assigning data points to bins, counting frequencies, and plotting the histogram. Effective interpretation and the application of best practices can transform a histogram into a powerful tool for data analysis and visualization, offering insights into the distribution, central tendency, and variability of the data. By understanding how to construct and interpret histograms, analysts and researchers can better communicate their findings and make data-driven decisions.