Calculating rotational inertia, also known as moment of inertia, is a fundamental concept in physics that describes an object's resistance to changes in its rotational motion. The moment of inertia depends on the object's mass distribution and the axis of rotation. Understanding how to calculate rotational inertia is crucial for analyzing and predicting the behavior of rotating systems in various fields, including engineering, astronomy, and particle physics.
Understanding the Concept of Rotational Inertia
Rotational inertia is a measure of how difficult it is to change the rotational motion of an object. The more mass an object has and the farther this mass is from the axis of rotation, the higher its moment of inertia. This concept is analogous to mass in linear motion, where the more massive an object is, the more resistant it is to changes in its linear velocity. The formula for rotational inertia (I) can be derived from the basic principles of rotational kinematics and dynamics, and it varies depending on the shape and mass distribution of the object.
Key Points
- The formula for rotational inertia depends on the object's geometry and the axis of rotation.
- For simple geometric shapes, specific formulas can be used to calculate the moment of inertia.
- For more complex shapes, the moment of inertia can be calculated by integrating the differential elements of mass over the entire object.
- The parallel axis theorem and the perpendicular axis theorem are useful for calculating the moment of inertia about different axes.
- Understanding rotational inertia is crucial for solving problems in rotational dynamics.
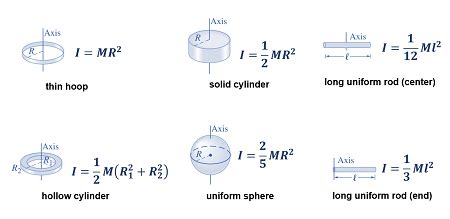
Formulas for Rotational Inertia of Common Shapes
For certain symmetric shapes, the moment of inertia can be calculated using specific formulas. These formulas are derived by integrating the differential elements of mass (dm) over the entire object, where r is the distance from the axis of rotation to the differential mass element, and the integral is taken over the entire mass of the object. Some common formulas include:
- Solid Sphere: (I = \frac{2}{5}MR^2), where M is the mass of the sphere and R is its radius.
- Hollow Sphere: (I = \frac{2}{3}MR^2), where M is the mass of the sphere and R is its radius.
- Cylinder: (I = \frac{1}{2}MR^2), for rotation about its central axis, where M is the mass of the cylinder and R is its radius.
- Rectangular Plate: (I = \frac{1}{12}M(a^2 + b^2)), for rotation about an axis perpendicular to the plate and through its center, where M is the mass of the plate, and a and b are its dimensions.
| Shape | Moment of Inertia Formula |
|---|---|
| Solid Sphere | \frac{2}{5}MR^2 |
| Hollow Sphere | \frac{2}{3}MR^2 |
| Cylinder | \frac{1}{2}MR^2 |
| Rectangular Plate | \frac{1}{12}M(a^2 + b^2) |

Calculating Rotational Inertia for Complex Shapes
For more complex shapes, the moment of inertia can be found by dividing the object into simpler shapes whose moments of inertia are known, and then summing these contributions. Alternatively, for objects with a continuous mass distribution, the moment of inertia can be calculated by integrating the differential mass elements over the volume of the object. The parallel axis theorem, which states (I = I{CM} + Md^2), where (I{CM}) is the moment of inertia about the center of mass, M is the total mass, and d is the distance from the axis of rotation to the center of mass, is particularly useful for calculating the moment of inertia about different axes.
Practical Applications of Rotational Inertia
Understanding and calculating rotational inertia has numerous practical applications. In engineering, it’s crucial for designing rotating machinery, such as engines and turbines, to ensure stability and efficiency. In sports, the concept of rotational inertia explains why figure skaters increase their spin rate by bringing their arms closer to their body. In space exploration, the moment of inertia of satellites and spacecraft is critical for their stability and maneuverability.
The calculation of rotational inertia is a fundamental skill in physics and engineering, allowing for the analysis and prediction of the behavior of rotating objects. By applying the appropriate formulas and theorems, such as the parallel axis theorem, one can determine the moment of inertia for a wide range of objects and scenarios, facilitating the design, optimization, and operation of rotating systems in various fields.
What is the difference between rotational inertia and linear inertia?
+Rotational inertia refers to an object’s resistance to changes in its rotational motion, while linear inertia refers to its resistance to changes in its linear motion. Both concepts relate to Newton’s first law of motion but apply to different types of motion.
How does the distribution of mass affect rotational inertia?
+The distribution of mass affects rotational inertia significantly. The farther the mass is from the axis of rotation, the greater the moment of inertia. This is why a figure skater spins faster when they bring their arms closer to their body, reducing their moment of inertia.
What is the parallel axis theorem, and how is it used?
+The parallel axis theorem states that the moment of inertia about any axis is equal to the moment of inertia about the center of mass plus the product of the mass and the square of the distance from the center of mass to the axis of rotation. This theorem is useful for calculating the moment of inertia about different axes, given the moment of inertia about the center of mass.