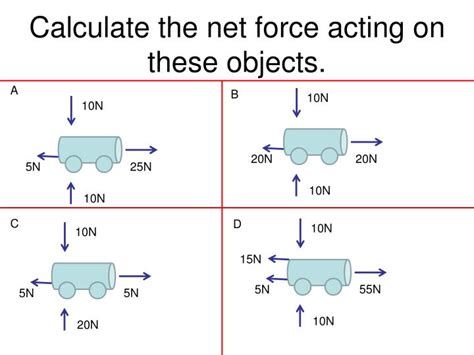
Calculating net force is a fundamental concept in physics, crucial for understanding the behavior of objects under the influence of multiple forces. The net force, also known as the resultant force, is the vector sum of all the forces acting on an object. It determines the acceleration of the object, according to Newton's second law of motion, which states that the acceleration of an object is directly proportional to the net force acting upon the object and inversely proportional to its mass. The formula for Newton's second law is F = ma, where F is the net force applied to the object, m is the mass of the object, and a is the acceleration produced.
Understanding the Components of Net Force Calculation

To calculate the net force, one must first identify all the forces acting on the object. These forces can be categorized into external forces, such as friction, gravity, and applied forces, and internal forces, which are not typically considered in net force calculations since they cancel each other out. For example, in a tug-of-war, the forces exerted by the participants on the rope are external forces relative to the rope, while the forces within the rope itself (e.g., the tension forces between its fibers) are internal and do not contribute to the net force acting on the rope as a whole.
Identifying Forces
Identifying the forces acting on an object involves understanding the environment and the interactions of the object with its surroundings. For instance, a block sliding down an inclined plane experiences several forces: the force of gravity pulling it downwards, the normal force exerted by the plane on the block (which is perpendicular to the plane’s surface), and possibly frictional forces opposing the motion. Each of these forces must be considered in calculating the net force.
| Force Type | Description | Direction |
|---|---|---|
| Gravity | Force due to gravitational attraction | Downwards |
| Normal Force | Force exerted by a surface on an object | Perpendicular to the surface |
| Frictional Force | Force opposing motion between two surfaces | Opposite to the direction of motion |

Vector Addition of Forces

The net force (F_net) is calculated by adding all the individual forces acting on an object. If the forces are given in terms of their components (e.g., x and y components in a 2D plane), the net force can be found by separately adding the x components and the y components of all forces, and then using the Pythagorean theorem to find the magnitude of the net force vector, if necessary.
Mathematically, if we have forces F1, F2,..., Fn acting on an object, the net force F_net is given by:
F_net = F1 + F2 +... + Fn
This vector equation can be broken down into component form for easier calculation, especially in 2D or 3D space:
F_net,x = F1,x + F2,x +... + F_n,x
F_net,y = F1,y + F2,y +... + F_n,y
For forces given in magnitude and direction (polar form), it's often necessary to convert them into component form (rectangular form) before adding them together.
Key Points for Calculating Net Force
- Identify all forces acting on the object, including their magnitudes and directions.
- Convert forces into a common coordinate system for easier addition.
- Add the forces vectorially, considering their directions.
- Apply Newton's second law of motion to relate the net force to the acceleration of the object.
- Consider the vector nature of forces and perform calculations accordingly.
Practical Applications and Considerations
In real-world scenarios, calculating the net force is essential for understanding and predicting the motion of objects. For instance, in engineering, the net force on a structure or a machine component determines its stability and performance. In transportation, understanding the net force on a vehicle helps in designing safer and more efficient vehicles. The concept of net force also applies to complex systems, such as the human body, where forces from muscles, bones, and external factors interact to produce movement and maintain posture.
The calculation of net force must consider all relevant forces and accurately account for their directions and magnitudes. In many cases, simplifications or assumptions are made to facilitate calculations, such as neglecting air resistance in projectile motion problems or assuming a frictionless surface. However, in precise engineering or scientific applications, all significant forces must be considered for accurate predictions.
What is the importance of calculating the net force in physics?
+Calculating the net force is crucial because it determines the acceleration of an object, according to Newton's second law of motion. Understanding the net force acting on an object allows us to predict its motion and design systems that can control or manipulate this motion.
How do you calculate the net force on an object with multiple forces acting on it?
+To calculate the net force, you must identify all the forces acting on the object, convert them into a common coordinate system if necessary, and then add them vectorially. This can be done by adding the components of the forces (e.g., x and y components) separately and then combining these components to find the net force vector.
What are some common forces to consider when calculating the net force?
+Common forces include gravity, normal force (the force exerted by a surface on an object), frictional forces (which oppose motion), and applied forces (such as the force exerted by a person pushing or pulling an object). The specific forces to consider depend on the context and the object in question.
In conclusion, calculating the net force is a fundamental skill in physics and engineering, requiring a thorough understanding of the forces acting on an object and how to add them vectorially. By applying the principles outlined here, one can accurately determine the net force acting on an object and predict its resulting motion, which is essential for a wide range of applications from designing machinery to understanding natural phenomena.