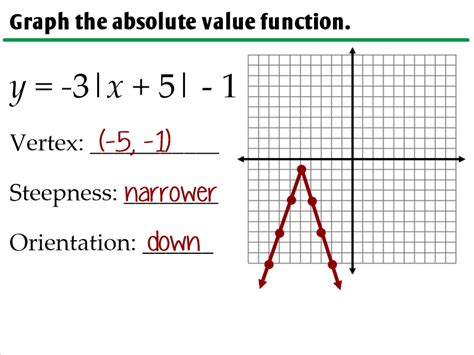
Graphing absolute value functions is a fundamental concept in algebra and mathematics, allowing students to visualize and understand the behavior of these functions. Absolute value functions are defined as f(x) = |x|, where the absolute value of a number is its distance from zero on the number line, regardless of direction. In this article, we will delve into the world of graphing absolute value functions, exploring their characteristics, key features, and practical applications.
Key Points
- Absolute value functions are defined as f(x) = |x|, where the absolute value of a number is its distance from zero on the number line.
- The graph of an absolute value function has a characteristic V-shape, with the vertex at the origin (0,0).
- Absolute value functions can be graphed using a variety of methods, including the use of tables, graphs, and algebraic manipulations.
- Transformations of absolute value functions, such as shifts and stretches, can be used to model real-world phenomena.
- Absolute value functions have numerous practical applications in fields such as physics, engineering, and economics.
Characteristics of Absolute Value Functions

Absolute value functions have several key characteristics that distinguish them from other types of functions. The graph of an absolute value function has a characteristic V-shape, with the vertex at the origin (0,0). This is because the absolute value of a number is always non-negative, so the function values are always greater than or equal to zero. Additionally, the graph of an absolute value function is symmetric about the y-axis, meaning that f(-x) = f(x) for all x in the domain.
The absolute value function can be defined piecewise as:
f(x) = x, if x ≥ 0
f(x) = -x, if x < 0
This definition allows us to graph the absolute value function by graphing the two separate pieces, x and -x, and combining them to form the V-shape.
Graphing Absolute Value Functions
There are several methods for graphing absolute value functions, including the use of tables, graphs, and algebraic manipulations. One common method is to use a table to generate values of the function for different inputs, and then plot these points on a graph. For example, to graph the function f(x) = |x|, we can generate the following table:
| x | f(x) = |x| |
|---|---|
| -3 | 3 |
| -2 | 2 |
| -1 | 1 |
| 0 | 0 |
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
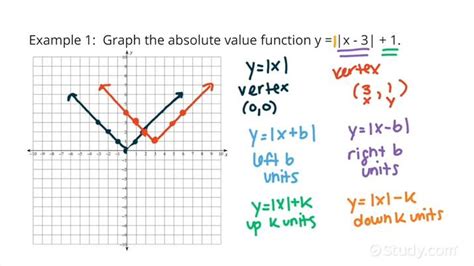
Plotting these points on a graph, we can see the characteristic V-shape of the absolute value function.
Transformations of Absolute Value Functions
Absolute value functions can be transformed in a variety of ways, including shifts and stretches, to model real-world phenomena. For example, the function f(x) = |x - 2| + 3 represents a shift of the absolute value function 2 units to the right and 3 units up. This type of transformation can be used to model situations such as the distance between two objects, where the absolute value function represents the distance and the shift represents the initial position of the objects.
Another example of a transformation of an absolute value function is the function f(x) = 2|x|, which represents a stretch of the absolute value function by a factor of 2. This type of transformation can be used to model situations such as the force exerted on an object, where the absolute value function represents the force and the stretch represents the magnitude of the force.
Practical Applications of Absolute Value Functions
Absolute value functions have numerous practical applications in fields such as physics, engineering, and economics. For example, in physics, the absolute value function can be used to model the distance between two objects, as mentioned earlier. In engineering, the absolute value function can be used to model the stress on a material, where the absolute value function represents the stress and the transformations represent the different types of stress, such as tension and compression.
In economics, the absolute value function can be used to model the cost of producing a good, where the absolute value function represents the cost and the transformations represent the different types of costs, such as fixed and variable costs. These are just a few examples of the many practical applications of absolute value functions.
What is the definition of an absolute value function?
+An absolute value function is defined as f(x) = |x|, where the absolute value of a number is its distance from zero on the number line.
How do you graph an absolute value function?
+There are several methods for graphing absolute value functions, including the use of tables, graphs, and algebraic manipulations. One common method is to use a table to generate values of the function for different inputs, and then plot these points on a graph.
What are some practical applications of absolute value functions?
+Absolute value functions have numerous practical applications in fields such as physics, engineering, and economics. For example, in physics, the absolute value function can be used to model the distance between two objects. In engineering, the absolute value function can be used to model the stress on a material. In economics, the absolute value function can be used to model the cost of producing a good.
In conclusion, graphing absolute value functions is an essential skill for students to develop, as it provides a foundation for understanding more complex mathematical concepts and models. Absolute value functions have numerous practical applications in fields such as physics, engineering, and economics, and can be transformed in a variety of ways to model real-world phenomena. By understanding the characteristics, key features, and practical applications of absolute value functions, students can develop a deeper appreciation for the beauty and power of mathematics.