Fractions and percents are fundamental concepts in mathematics, playing a crucial role in various aspects of our lives, from simple calculations to complex financial transactions. Understanding the relationship between fractions and percents is essential for problem-solving and decision-making in numerous fields, including science, economics, and engineering. In this article, we will delve into the world of fractions and percents, exploring their definitions, interconversion, and practical applications.
Key Points
- Fractions represent a part of a whole, consisting of a numerator and a denominator.
- Percents are a way to express a fraction with a denominator of 100, denoted by the % symbol.
- Converting fractions to percents involves dividing the numerator by the denominator and multiplying by 100.
- Converting percents to fractions requires dividing the percent value by 100 and simplifying the resulting fraction.
- Fractions and percents have numerous practical applications in real-world scenarios, including finance, science, and engineering.
Understanding Fractions

Fractions are mathematical expressions that represent a part of a whole. They consist of two main components: the numerator (the top number) and the denominator (the bottom number). The numerator indicates the number of equal parts, while the denominator represents the total number of parts that make up the whole. For instance, the fraction 3⁄4 represents 3 equal parts out of a total of 4 parts. Fractions can be classified into different types, including proper fractions (where the numerator is less than the denominator), improper fractions (where the numerator is greater than or equal to the denominator), and mixed numbers (which combine a whole number with a fraction).
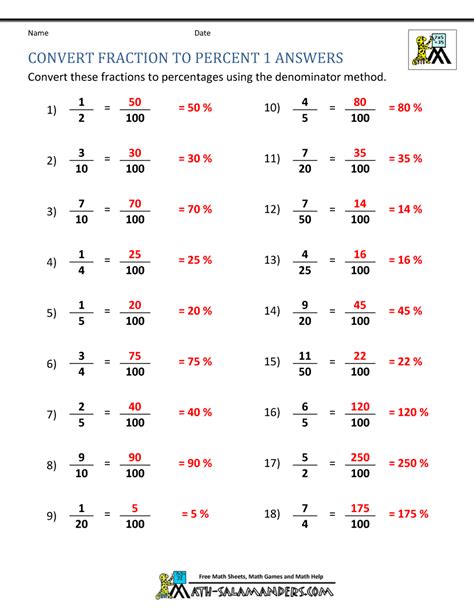
Converting Fractions to Percents
To convert a fraction to a percent, we need to divide the numerator by the denominator and then multiply the result by 100. This process can be represented by the formula: (numerator ÷ denominator) × 100 = percent. For example, to convert the fraction 3⁄4 to a percent, we would perform the following calculation: (3 ÷ 4) × 100 = 75%. This means that the fraction 3⁄4 is equivalent to 75%.
| Fraction | Percent |
|---|---|
| 1/2 | 50% |
| 1/4 | 25% |
| 3/4 | 75% |
| 2/3 | 66.67% |

Understanding Percents

Percents are a way to express a fraction with a denominator of 100. The % symbol is used to denote a percent, and it represents a ratio of a part to a whole. Percents are commonly used in various real-world applications, such as finance, science, and engineering. For instance, a 25% discount on a product means that the customer will pay 75% of the original price.
Converting Percents to Fractions
To convert a percent to a fraction, we need to divide the percent value by 100 and then simplify the resulting fraction. This process can be represented by the formula: (percent ÷ 100) = fraction. For example, to convert 75% to a fraction, we would perform the following calculation: 75 ÷ 100 = 0.75, which can be simplified to 3⁄4. This means that 75% is equivalent to the fraction 3⁄4.
What is the difference between a fraction and a percent?
+A fraction represents a part of a whole, while a percent is a way to express a fraction with a denominator of 100.
How do I convert a fraction to a percent?
+To convert a fraction to a percent, divide the numerator by the denominator and multiply the result by 100.
What is the formula for converting a percent to a fraction?
+The formula for converting a percent to a fraction is: (percent ÷ 100) = fraction.
In conclusion, fractions and percents are interconnected concepts that play a vital role in various aspects of mathematics and real-world applications. Understanding the relationship between fractions and percents is crucial for problem-solving and decision-making in numerous fields. By mastering the conversion processes between fractions and percents, individuals can develop a deeper understanding of mathematical concepts and improve their ability to analyze and interpret data.