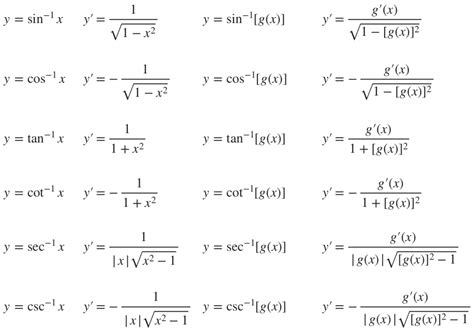The derivative of arc trig functions is a fundamental concept in calculus, particularly in the realm of inverse trigonometric functions. Arc trig functions, also known as inverse trig functions, are used to determine the angle whose trigonometric function is a given value. The derivatives of these functions are crucial in various mathematical and real-world applications, including optimization problems, physics, and engineering. In this article, we will delve into the derivatives of arc trig functions, exploring their definitions, formulas, and applications.
Introduction to Arc Trig Functions

Arc trig functions are the inverses of the basic trigonometric functions: sine, cosine, and tangent. They are denoted as arcsin(x), arccos(x), and arctan(x), respectively. These functions return the angle whose sine, cosine, or tangent is the given value x. For instance, arcsin(x) gives the angle whose sine is x. The range of arc trig functions is restricted to ensure they are one-to-one functions, which is necessary for their inverses to be well-defined.
Derivatives of Arc Trig Functions
The derivatives of arc trig functions can be derived using the inverse function rule, which states that if f(x) is a one-to-one function with an inverse f^(-1)(x), then the derivative of f^(-1)(x) is given by 1 / f’(f^(-1)(x)). Applying this rule to the arc trig functions yields the following derivatives:
- The derivative of arcsin(x) is 1 / sqrt(1 - x^2)
- The derivative of arccos(x) is -1 / sqrt(1 - x^2)
- The derivative of arctan(x) is 1 / (1 + x^2)
These derivatives are essential in calculus, as they enable us to find the rates of change of arc trig functions with respect to their arguments.
Key Points
- The derivative of arcsin(x) is 1 / sqrt(1 - x^2)
- The derivative of arccos(x) is -1 / sqrt(1 - x^2)
- The derivative of arctan(x) is 1 / (1 + x^2)
- Arc trig functions are used to determine the angle whose trigonometric function is a given value
- The derivatives of arc trig functions are crucial in various mathematical and real-world applications
Applications of Arc Trig Functions and Their Derivatives
Arc trig functions and their derivatives have numerous applications in mathematics, physics, and engineering. In physics, for example, arc trig functions are used to determine the angle of projection of a projectile, while their derivatives are used to find the rate of change of this angle with respect to time. In engineering, arc trig functions are used in the design of electronic circuits, such as filters and amplifiers, where the phase shift of a signal is critical.
Optimization Problems
Arc trig functions and their derivatives are also used in optimization problems, where the goal is to maximize or minimize a function subject to certain constraints. For instance, in the design of a radar system, the goal may be to maximize the range of the radar while minimizing the power consumption. Arc trig functions and their derivatives can be used to find the optimal angle of elevation of the radar antenna to achieve this goal.
| Function | Derivative | Application |
|---|---|---|
| arcsin(x) | 1 / sqrt(1 - x^2) | Projectile motion, radar systems |
| arccos(x) | -1 / sqrt(1 - x^2) | Electronic circuits, filter design |
| arctan(x) | 1 / (1 + x^2) | Optimization problems, signal processing |
Conclusion
In conclusion, the derivatives of arc trig functions are fundamental concepts in calculus, with numerous applications in mathematics, physics, and engineering. Understanding these derivatives is crucial for solving optimization problems, designing electronic circuits, and modeling real-world phenomena. By applying the inverse function rule and using the derivatives of arc trig functions, we can find the rates of change of these functions and make informed decisions in a wide range of fields.
What is the derivative of arcsin(x)?
+The derivative of arcsin(x) is 1 / sqrt(1 - x^2)
What is the derivative of arccos(x)?
+The derivative of arccos(x) is -1 / sqrt(1 - x^2)
What is the derivative of arctan(x)?
+The derivative of arctan(x) is 1 / (1 + x^2)