The cross product and dot product are two fundamental operations in vector mathematics, playing crucial roles in various fields such as physics, engineering, and computer graphics. Understanding the differences and applications of these two products is essential for navigating complex mathematical and real-world problems. In this article, we will delve into the definitions, calculations, and uses of the cross product and dot product, providing a comprehensive overview for those seeking to grasp these concepts.
Key Points
- The cross product of two vectors results in a new vector that is perpendicular to both original vectors.
- The dot product of two vectors yields a scalar value, representing the amount of "similarity" between the vectors in terms of direction.
- Both products are used extensively in physics and engineering to describe forces, torques, and work done.
- The cross product is utilized in calculating the area of parallelograms and the volume of parallelepipeds, while the dot product is used in determining the projection of one vector onto another.
- Understanding the geometric and algebraic interpretations of these products is crucial for problem-solving in vector mathematics.
Introduction to Vector Products

Vectors are mathematical objects that possess both magnitude and direction, making them ideal for describing quantities such as displacement, velocity, and acceleration. The cross product and dot product are operations that combine two vectors to produce either another vector or a scalar, depending on the operation. These products are not only essential for advancing in mathematics but also have practical applications in fields like robotics, where the manipulation of objects in 3D space requires precise calculations of forces and torques.
Cross Product
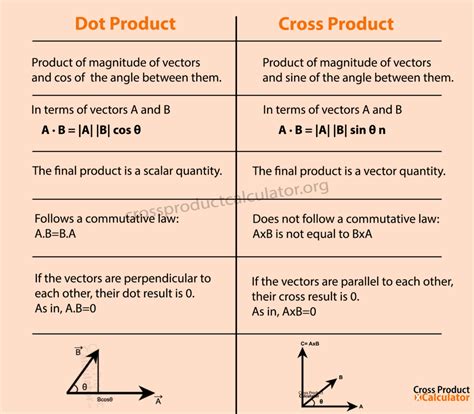
The cross product of two vectors a and b, denoted as a × b, results in a vector that is perpendicular to both a and b. The magnitude of the resulting vector is given by the product of the magnitudes of a and b and the sine of the angle between them. The formula for the cross product is:
a × b = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1), where a = (a1, a2, a3) and b = (b1, b2, b3). This operation is anticommutative, meaning a × b = -b × a.
The cross product is crucial in physics for calculating the torque exerted by a force, the angular momentum of an object, and the magnetic field generated by a current-carrying wire. It’s also used in computer graphics to perform rotations and to determine the normal vectors of surfaces, which is vital for rendering and lighting calculations.
Dot Product
The dot product of two vectors a and b, denoted as a · b, results in a scalar value. It can be calculated using the formula a · b = a1b1 + a2b2 + a3b3, where a = (a1, a2, a3) and b = (b1, b2, b3). The dot product is commutative, meaning a · b = b · a. The dot product can also be expressed as a · b = |a| |b| cos(θ), where |a| and |b| are the magnitudes of vectors a and b, respectively, and θ is the angle between them.
The dot product is essential for determining the work done by a force on an object, the power transferred, and the projection of one vector onto another. It’s also a key component in the calculation of the cosine of the angle between two vectors, which can be used to measure the similarity in direction between the vectors.
| Product | Result | Formula | Application |
|---|---|---|---|
| Cross Product | Vector | a × b = (a2b3 - a3b2, a3b1 - a1b3, a1b2 - a2b1) | Torque, Angular Momentum, Magnetic Field |
| Dot Product | Scalar | a · b = a1b1 + a2b2 + a3b3 or a · b = |a| |b| cos(θ) | Work Done, Power, Vector Projection |

Applications and Implications

The cross and dot products have far-reaching implications in various fields. In physics, they are used to describe the fundamental laws governing the behavior of objects under the influence of forces and fields. In engineering, these products are crucial for the design of machines, mechanisms, and electronic circuits. In computer graphics, they enable the creation of realistic 3D models and simulations.
Furthermore, the cross product is used in the calculation of the volume of a parallelepiped, which is essential in architecture and construction for determining the volume of buildings and structures. The dot product, on the other hand, is vital in signal processing, where it is used to measure the similarity between signals, which has applications in pattern recognition and machine learning.
Conclusion and Future Directions
In conclusion, the cross product and dot product are not only fundamental mathematical operations but also have profound implications in various fields. Understanding these products and their applications is essential for advancing in mathematics, physics, engineering, and computer science. As technology continues to evolve, the importance of vector mathematics will only grow, with potential future directions including advanced applications in quantum mechanics, artificial intelligence, and materials science.
What is the primary difference between the cross product and dot product?
+The primary difference is that the cross product results in a vector, while the dot product yields a scalar. The cross product vector is perpendicular to both original vectors, whereas the dot product scalar represents the amount of "similarity" in direction between the two vectors.
How are the cross and dot products used in physics?
+In physics, the cross product is used to calculate torque, angular momentum, and the magnetic field generated by a current. The dot product is used to calculate the work done by a force, the power transferred, and the projection of one vector onto another.
What are some practical applications of vector products in engineering?
+Practical applications include the design of machines, mechanisms, and electronic circuits, where understanding the forces, torques, and energy transfers is crucial. Vector products are also essential in computer graphics for 3D modeling and simulations.
By grasping the concepts of the cross product and dot product, individuals can enhance their understanding of vector mathematics and its applications, paving the way for advancements in various scientific and engineering disciplines.