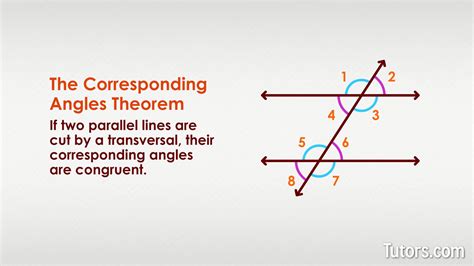
The Corresponding Angles Theorem, also known as the Corresponding Angles Postulate, is a fundamental concept in geometry that describes the relationship between angles formed when a transversal intersects two lines. This theorem is crucial in understanding various geometric properties and is widely used in proofs and problem-solving in mathematics. The Corresponding Angles Theorem states that if two lines are cut by a transversal and the corresponding angles are congruent, then the two lines are parallel. In this article, we will delve into the details of the Corresponding Angles Theorem, its proof, and its applications, while also exploring related concepts such as alternate interior angles and alternate exterior angles.
Key Points
- The Corresponding Angles Theorem states that if two lines are cut by a transversal and the corresponding angles are congruent, then the two lines are parallel.
- The theorem is used to prove that two lines are parallel, and it is a fundamental concept in geometry.
- Corresponding angles are angles that are in the same relative position in two different intersections.
- Alternate interior angles and alternate exterior angles are also used to determine if two lines are parallel.
- The Corresponding Angles Theorem has various applications in geometry, trigonometry, and engineering.
Understanding Corresponding Angles

Corresponding angles are angles that are in the same relative position in two different intersections. When a transversal intersects two lines, it forms several pairs of angles. The corresponding angles are the angles that are in the same position in each intersection. For example, if a transversal intersects two lines, the upper left angle and the lower right angle are corresponding angles. The Corresponding Angles Theorem states that if these corresponding angles are congruent, then the two lines are parallel.
Proof of the Corresponding Angles Theorem
The proof of the Corresponding Angles Theorem involves showing that if the corresponding angles are congruent, then the two lines are parallel. This can be done using various methods, including using the concept of alternate interior angles and alternate exterior angles. One way to prove the theorem is to assume that the two lines are not parallel and then show that this leads to a contradiction. This proof requires a deep understanding of geometric concepts and the ability to apply logical reasoning.
| Angle Type | Description |
|---|---|
| Corresponding Angles | Angles that are in the same relative position in two different intersections. |
| Alternate Interior Angles | Angles that are on opposite sides of the transversal and inside the two lines. |
| Alternate Exterior Angles | Angles that are on opposite sides of the transversal and outside the two lines. |

Applications of the Corresponding Angles Theorem
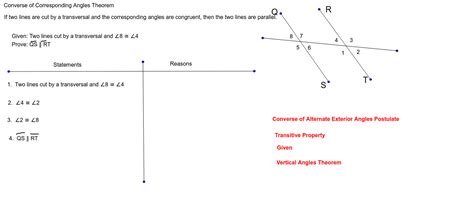
The Corresponding Angles Theorem has various applications in geometry, trigonometry, and engineering. One of the primary applications is in proving that two lines are parallel. The theorem is also used in constructing parallel lines and in solving problems involving parallel lines and transversals. In addition, the Corresponding Angles Theorem is used in trigonometry to solve problems involving right triangles and in engineering to design and construct parallel structures.
Alternate Interior and Exterior Angles
Alternate interior angles and alternate exterior angles are also used to determine if two lines are parallel. Alternate interior angles are angles that are on opposite sides of the transversal and inside the two lines. Alternate exterior angles are angles that are on opposite sides of the transversal and outside the two lines. If the alternate interior angles or alternate exterior angles are congruent, then the two lines are parallel. This is another way to prove that two lines are parallel, and it is often used in conjunction with the Corresponding Angles Theorem.
What is the Corresponding Angles Theorem?
+The Corresponding Angles Theorem states that if two lines are cut by a transversal and the corresponding angles are congruent, then the two lines are parallel.
What are corresponding angles?
+Corresponding angles are angles that are in the same relative position in two different intersections.
What are alternate interior angles and alternate exterior angles?
+Alternate interior angles are angles that are on opposite sides of the transversal and inside the two lines. Alternate exterior angles are angles that are on opposite sides of the transversal and outside the two lines.
In conclusion, the Corresponding Angles Theorem is a fundamental concept in geometry that describes the relationship between angles formed when a transversal intersects two lines. The theorem is used to prove that two lines are parallel, and it has various applications in geometry, trigonometry, and engineering. Understanding the Corresponding Angles Theorem and its applications is essential for anyone interested in mathematics and geometry. By applying the theorem and its related concepts, individuals can solve problems involving parallel lines and transversals, and gain a deeper understanding of geometric properties and relationships.