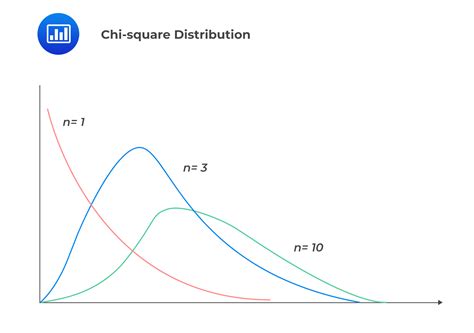
The Chi Squared distribution, denoted as χ², is a fundamental concept in statistics, particularly in the realm of hypothesis testing and confidence intervals. It is a continuous probability distribution that is widely used in statistical inference, especially when dealing with categorical data or when the data follows a normal distribution. The Chi Squared distribution is closely related to the normal distribution and is used to describe the distribution of the sum of the squares of independent standard normal random variables.
Key Points
- The Chi Squared distribution is used for hypothesis testing, confidence intervals, and regression analysis.
- The distribution is characterized by its degrees of freedom, which determine its shape and scale.
- The Chi Squared test is used to determine whether there is a significant difference between observed and expected frequencies.
- The distribution is asymmetric and skewed to the right, with the degree of skewness decreasing as the degrees of freedom increase.
- The Chi Squared distribution is used in various fields, including medicine, social sciences, and engineering.
Properties of the Chi Squared Distribution
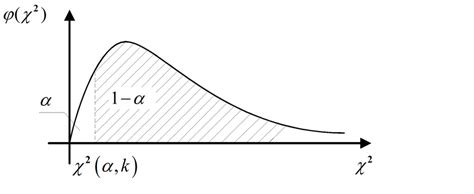
The Chi Squared distribution has several key properties that make it useful in statistical analysis. One of the most important properties is its relationship to the normal distribution. If we have a set of independent standard normal random variables, the sum of their squares follows a Chi Squared distribution. The degrees of freedom of the Chi Squared distribution determine its shape and scale. For example, the Chi Squared distribution with one degree of freedom is equivalent to the square of a standard normal distribution.
Degrees of Freedom
The degrees of freedom of the Chi Squared distribution are a critical concept in understanding its properties. The degrees of freedom determine the number of independent pieces of information used to estimate a parameter. In the case of the Chi Squared distribution, the degrees of freedom are equal to the number of independent standard normal random variables that are squared and summed. For example, if we have a sample of size n, the degrees of freedom for the Chi Squared distribution would be n-1.
| Degree of Freedom | Description |
|---|---|
| 1 | Equivalent to the square of a standard normal distribution |
| 2 | Equivalent to the sum of the squares of two independent standard normal distributions |
| n | Equivalent to the sum of the squares of n independent standard normal distributions |

Applications of the Chi Squared Distribution
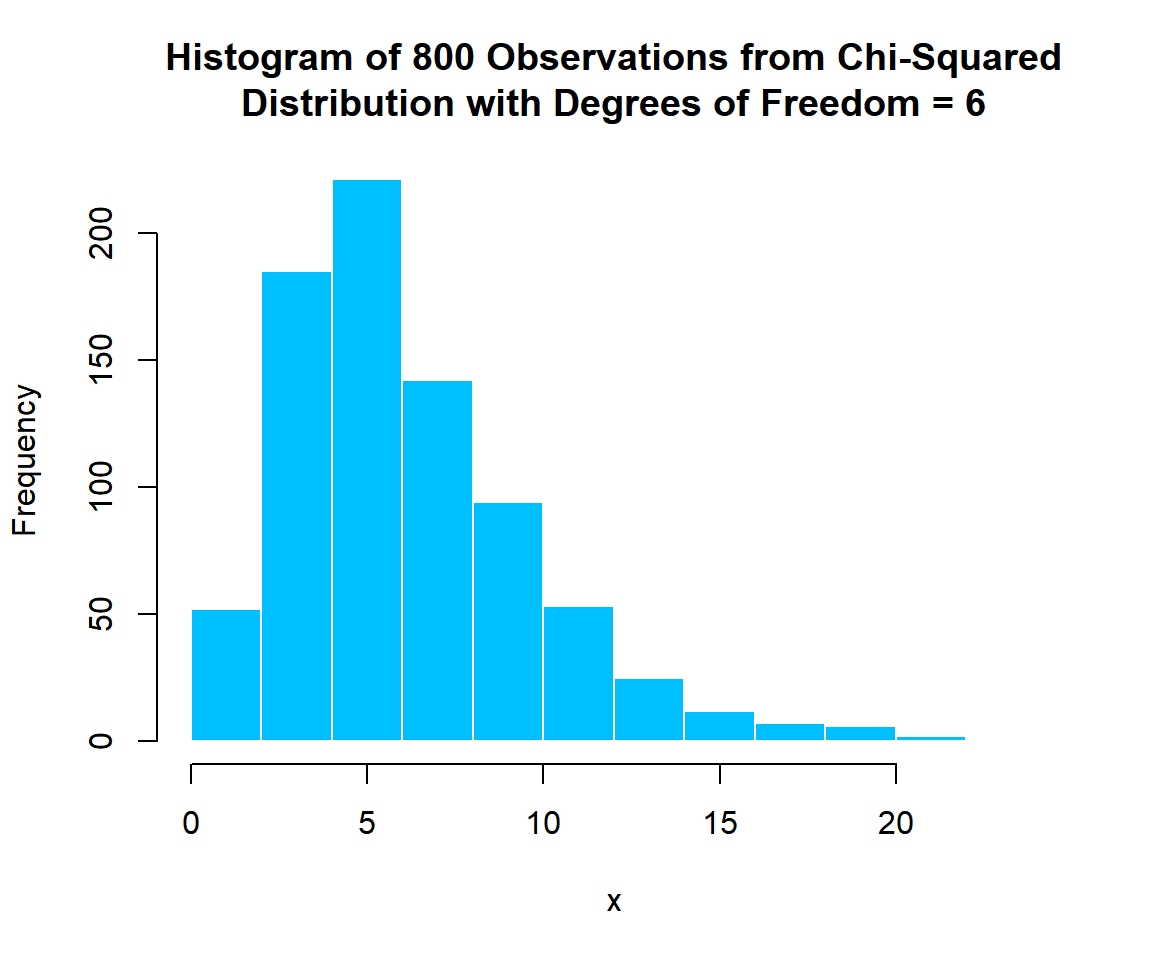
The Chi Squared distribution has numerous applications in statistics and data analysis. One of the most common uses is in hypothesis testing, particularly in tests of independence and goodness of fit. The Chi Squared test is used to determine whether there is a significant difference between observed and expected frequencies. The test is widely used in medicine, social sciences, and engineering to analyze categorical data.
Chi Squared Test
The Chi Squared test is a statistical test used to determine whether there is a significant difference between observed and expected frequencies. The test is based on the Chi Squared distribution and is used to test the null hypothesis that the observed frequencies are equal to the expected frequencies. The test statistic is calculated as the sum of the squared differences between the observed and expected frequencies, divided by the expected frequencies.
The Chi Squared distribution is also used in confidence intervals and regression analysis. In confidence intervals, the Chi Squared distribution is used to construct intervals for population parameters, such as the mean and variance. In regression analysis, the Chi Squared distribution is used to test the significance of regression coefficients and to construct confidence intervals for the coefficients.
What is the difference between the Chi Squared distribution and the normal distribution?
+The Chi Squared distribution is a continuous probability distribution that is used to describe the distribution of the sum of the squares of independent standard normal random variables. The normal distribution, on the other hand, is a continuous probability distribution that is used to describe the distribution of a single random variable.
How is the Chi Squared distribution used in hypothesis testing?
+The Chi Squared distribution is used in hypothesis testing to determine whether there is a significant difference between observed and expected frequencies. The Chi Squared test is used to test the null hypothesis that the observed frequencies are equal to the expected frequencies.
What are the degrees of freedom of the Chi Squared distribution?
+The degrees of freedom of the Chi Squared distribution are equal to the number of independent pieces of information used to estimate a parameter. In the case of the Chi Squared distribution, the degrees of freedom are equal to the number of independent standard normal random variables that are squared and summed.
In conclusion, the Chi Squared distribution is a fundamental concept in statistics, with numerous applications in hypothesis testing, confidence intervals, and regression analysis. Understanding the properties of the Chi Squared distribution, including its relationship to the normal distribution and its degrees of freedom, is critical in applying the distribution in practice. The Chi Squared distribution is a versatile tool in statistical analysis, and its applications continue to grow in various fields, including medicine, social sciences, and engineering.