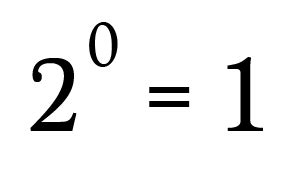The concept of exponentiation is a fundamental aspect of mathematics, and one of the most basic yet intriguing aspects of it is the behavior of numbers when raised to the power of 0. In this context, let's explore the notion of 3 to the power of 0, denoted as 3^0. Understanding this concept requires a brief excursion into the principles of exponentiation and how mathematicians define the result of raising any number to the zeroth power.
Definition of Exponentiation

Exponentiation is a mathematical operation that involves raising a number, known as the base, to a certain power, known as the exponent. The result of this operation is the base multiplied by itself as many times as the value of the exponent. For example, 3^4 means 3 multiplied by itself 4 times (3*3*3*3). However, when the exponent is 0, the operation doesn’t involve multiplication in the conventional sense because any number multiplied by itself zero times doesn’t intuitively suggest a clear result.
Mathematical Convention for Zero Exponent
In mathematics, a convention has been established to handle the case where the exponent is 0. This convention states that any non-zero number raised to the power of 0 equals 1. Thus, 3^0, following this convention, equals 1. This might seem arbitrary at first, but it’s a definition that has been adopted to ensure consistency and simplicity in various mathematical operations and identities.
| Base | Exponent | Result |
|---|---|---|
| 3 | 0 | 1 |
| 5 | 0 | 1 |
| 10 | 0 | 1 |

Key Points
- The concept of a number raised to the power of 0 is defined by convention in mathematics.
- Any non-zero number raised to the power of 0 equals 1, as per the established convention.
- This convention is essential for the consistency and applicability of various mathematical formulas and identities.
- The definition applies universally, meaning 3^0, 5^0, 10^0, or any other non-zero number raised to the 0 power, all equal 1.
- Understanding and applying this convention is fundamental in algebra, calculus, and other areas of mathematics.
Implications and Applications

The convention that any non-zero number to the power of 0 equals 1 has profound implications across various mathematical disciplines. In algebra, it simplifies the expression of polynomial equations and ensures that certain identities, like the binomial theorem, hold true for all values of the exponent. In calculus, understanding this convention is crucial for the application of limit rules and for simplifying expressions in the analysis of functions.
Historical Perspective
Historically, the development of the concept of zero as an exponent and its subsequent definition as resulting in 1 has evolved over time. Early mathematicians may not have explicitly addressed this issue, but as mathematics became more sophisticated and the need for consistency arose, the convention was formally adopted. This development reflects the dynamic nature of mathematics, where definitions and conventions are established to facilitate the development of theories and to ensure logical consistency.
Why is any non-zero number raised to the power of 0 defined as 1?
+This definition is a convention adopted in mathematics to maintain consistency in mathematical operations and identities. It ensures that various formulas and theorems work correctly for all values of the variables involved.
Does this convention apply to negative numbers as well?
+Yes, the convention applies to all non-zero numbers, whether positive or negative. For example, (-3)^0 equals 1, following the same convention.
Is this convention used in all mathematical operations?
+This convention is universally applied in mathematics to ensure consistency. However, it's particularly crucial in algebra and calculus, where it underpins various theorems and formulas.
In conclusion, the concept of 3 to the power of 0, or any non-zero number to the power of 0, being equal to 1 is a fundamental convention in mathematics. This convention ensures the consistency and applicability of mathematical formulas and identities, making it a cornerstone of mathematical theory and practice. As mathematics continues to evolve, understanding and applying this convention will remain essential for advancing our knowledge and solving complex problems across various disciplines.